zad adam: Z rozwartego kata rombu ABCD opuszczono wysokości na jego dwa boki. Długość każdej wysokości wynosi a, odległość między spodkami wysokości wynosi b. Wyznaczyć pole rombu.

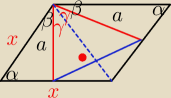
Basia: β=90−α 2β+2γ=180−α 2y = 180−α−2β 2γ=180−α−180+2α = α

	b
sin γ =
	2a

	√4a2−b2
cosγ= √1−b2/(4a2) =
	2a

	2b*√4a2−b2		b√4a2−b2
sinα = sin(2γ) = 2sinγ*cosγ =		=
	4a2		2a2

	a
sinα=
	x

	a
x =
	sinα

	a2		a2		4a2
P = x2*sinα =		*sinα =		=
	sin2α		sinα		b√4a2−b2

mogłam się pomylić w obliczeniach, poza tym prawdopodobnie jest jakiś prostszy sposób

Eta:

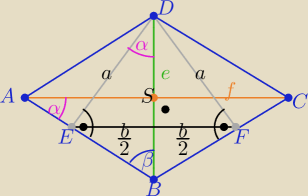
	e*f
P(rombu)=
	2

	a		a		b
w ΔDEB : e=		=		i sinα=
	sinβ		cosα		2a

	b2		√4a2−b2
to cos2α=1−sin2α= 1−		⇒ cosα=
	4a2		2a

	2a2
więc e=
	√4a2−b2

analogicznie wyznaczamy "f"

	e		a		2a2
w ΔABS :		=tgα ⇒ f=		to f =
	f		sinα		b

	1		2a2		2a2
P(rombu) =		*		*
	2		b		√4a2−b2

	4a4
P=
	b√4a2−b2

=============== Basi gdzieś umknęła.. a⁴

adam: z tw. cosinusów jest łatwiej

adam: powinno być być w liczniku 2a⁴ a nie 4a⁴