planimetria mk: Dłuższa podstawa trapezu prostokątnego ma długość a, krótsza zaś długość b. Wykaż, że odległość

	ab
punktu przecięcia przekątnych trapezu od krótszego ramienia jest równa		. Obrazka nie
	a+b

zrobie, bo nie wiem jak tu się to robi. Jak ktoś chce się pobawić z tym zadaniem z góry dziękuje. Ja próbowałam zrobić to przez podobieństwo trójkątów zawierających boki a i b, a potem z twierdzenia Talesa (tak podpowiadał internet), ale szukany x wyszedł mi równy a, więc coś się nie zgadza.

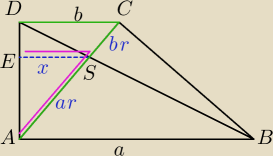
aniabb: ΔABS podobny do ΔCDS w skali a/b więc bok AS /SC =a/b

AC		AS
	=
DC		SE

(a+b)r		ar		ab
	=		więc x=
b		x		a+b

Mila:

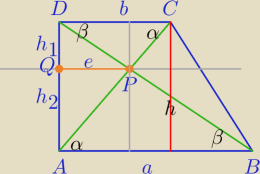
	b
1) ΔDCP∼ΔΔABP w skali k=		( cecha kkk)
	a

h=h₁+h₂

h1		b		b		a
	=		⇔h1=		*h2, h2=		*h1
h2		a		a		b

2) ΔPQD∼ΔBAD⇔

h1		h
	=		⇔e*h=h1*a
e		a

e*(h₁+h₂)=h₁*a

	a
e*(h1+		*h1)=h1*a
	b

	a
e*h1*(1+		)=h1*a
	b

	b+a
e*		=a
	b

	a*b
e=
	a+b

cnw ===========

mk: Dziękuje bardzo

Eta: To aniabb "pozamiatała" w dwu linijkach

Eta: Mogła jeszcze użyć zamiast ar .... ak, bk bo r −−− kojarzy się z promieniem okręgu wpisanego

aniabb: myślałam o ramieniu trójkąta

Eta: x −−− połowa średniej harmonicznej długości podstaw