RACHUNEK RÓŻNICZKOWY bluee: Na krzywej o równaniu xy=4 obrano punkty A=(1,4), B=(2,2) i C, przy czym obydwie współrzędne punktu C są ujemne. Wykaż, że pole ΔABC jest najmniejsze, gdy C=(−√2,−2√2).

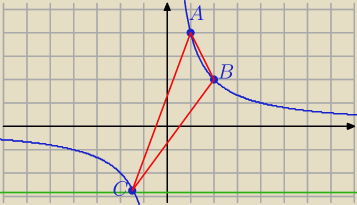
Janek191: A = ( 1,4) B = (2, 2)

	4
C = ( x,		)
	x

→

	4
CA = [ 1 − x, 4 −		]
	x

→

	4
CB = [ 2 − x, 2 −		]
	x

Pole Δ ABC → → P = 0,5* I det ( CA , CB ) I

	4		4		4
P(x) = 0,5 *I (1 − x)*( 2 −		) − (2 − x)*( 4 −		) I = I 2 x +		− 6 I
	x		x		x

	4
P ' (x) = 2 −		= 0 ⇔ x = −√2 lub x = √2 − minimum funkcji P(x)
	x2

Wtedy

	4
y =		= − 2√2
	−√2

C = ( − √2, − 2√2)

bluee: Co znaczy det?

Janek191: Wyznacznik pary wektorów.

bluee: Kompletnie nie wiem o co chodzi w tym rozwiązaniu. Z wektorów mieliśmy tylko dwie lekcje.

bluee: Czy można to rozwiązać inną metodą?

Jerzy: A czego nie rozumiesz ?

bluee: Do momentu wyznaczenia współrzędnych wektorów jest OK. Ale nie wiem jak wyprowadzono wzór na pole ΔABC.

Jerzy: To jest znany wzór na pole trójkąta. Pole trójkąta jest połową pola równoległoboku zbudowanego na dwóch wektorach,a pole równoległoboku to po prostu wartośc wyznacznika utworzonego ze współrzednych tych wektorów.

bluee: Ok, teraz już łapie, DZIĘKI