proszę o rozwiązanie
Anna: rozwiąż nierówność
2cos
2x < 1 gdzie x ∊ <0 ; 2π>
| | √2 | | √2 | |
czyli cosx < |
| lub cosx > − |
| |
| | 2 | | 2 | |
| | π | | π | |
x < |
| +kπ lub x > − |
| + kπ |
| | 4 | | 4 | |
7 mar 14:44
Jerzy:
Po pierwsze koniunkcja, po drugie inny okres.
7 mar 15:03
Anna: czyli
| | π | | π | |
x < |
| + 2kπ ∧ x < − |
| + 2kπ |
| | 4 | | 4 | |
7 mar 15:14
Jerzy:
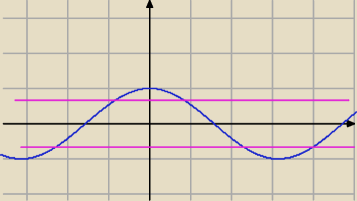
Różowe linnie, to: y =
√2/2 oraz y = −
√2/2
7 mar 15:23
Anna: dziękuję
7 mar 15:29
Jerzy:
Popraw rozwiązanie, bo jest niewłaściwe.
7 mar 15:32
Anna: nie wiem jak zapisać
7 mar 15:34
Jerzy:
Określ w jakim zakresie kątów niebieska linia leży pomiedzy różowymi.
7 mar 15:37
Anna: czyli
| | 5 | | π | | π | | 3 | |
x∊ (− |
| π; − |
| ) ∪ ( |
| ; |
| π) |
| | 4 | | 4 | | 4 | | 4 | |
7 mar 16:02
Anna: ale uwzględniając dziedzinę
| | π | | 3 | | 5 | | 7 | |
to x ∊ ( |
| ; |
| ) ∪ ( |
| π ; |
| π) |
| | 4 | | 4 | | 4 | | 4 | |
czy teraz dobrze
7 mar 16:08
Adamm:
2cos2x−1<0
cos(2x)<0
i zadanko okazało się bardzo proste
7 mar 16:20
Anna: a jaki jest zbiór rozwiązań
7 mar 16:32