największa wartość funkcji 3 stopnia abcd: Największa wartość funkcji f(x) = 1 + 12x− x³ A) jest równa 17 B) jest równa −15 C) jest równa 4 D) nie istnieje Odpowiedź to D. Ja wyznaczyłam pochodną f'(x)= 3(4−x²)=3(2−x)(2+x). wyszło mi, że dla x=2 jest maksimum lokalne. f(2)=17, ale jest to źle. Dlaczego moje rozwiązanie jest złe i jak należało zrobić to zadanie i dlaczego? Proszę o pomoc, dziękuję

iteRacj@: zauważ, że lim_x→−∞ (1+12x−x³) = ∞

xxx: Bo przy x → −nieskończoność, wartość funkcji dąży do nieskończoności

iteRacj@: znalazłaś maksimum lokalne a to co innego niż największa wartość funkcji

abcd: nadal nie rozumiem... dlaczego sprawdzamy granicę przy −nieskończoności?

abcd: a nie +nieskończoności?

iteRacj@: szukając największej wartości funkcji musisz sprawdzić nie tylko maksima lokalne, ale również obliczyć granice na krańcach dziedziny, porównać je i wybrać wartość większą

the foxi: Współczynnik przy x³ jest ujemny, więc to funkcja stale malejąca Zatem gdzie można się spodziewać największej wartości? :v

iteRacj@: czyli sprawdzasz obie granice i porównujesz

abcd: Ok, a w przypadku maksimum lokalnego liczę tylko pochodną i rozwiązuję tak, jak napisałam w pierwszym poście, tak?

iteRacj@: jeśli masz polecenie, żeby znaleźć maksima lokalne to tak, jak napisałaś: obliczasz pochodną i sprawdzasz, kiedy zmienia znak ale jeśli szukasz największej wartości funkcji, to jeszcze liczysz granice (czasem trzeba policzyć więcej niż dwie)

abcd: Baaardzo dziękuję wszystkim za pomoc (szczególnie iteRacj@)! teraz już wszystko jasne Miłego wieczoru!

Hmm: Krancami dziedziny są −∞ i ∞ czego nie badamy granicy w + ∞ tylko w −∞?

Basia: skróty myślowe to są

	12		1
limx→+∞ (−x3+12x+1) = limx→+∞ x3(−1+		+		) =
	x2		x3

+∞(−1+0+0) = +∞*(−1) = −∞ więc dla wartości największej nieistotne

iteRacj@: obliczamy obie granice w −∞ i ∞, ale szukamy największej wartości funkcji, to granicy x→∞ nie bierzemy pod uwagę, bo od razu widać, że są wieksze od niej wartości funkcji

Hmm: Dzięki a jeżeli dziedzina jest R−{1} to badamy granice w +/−∞ i 1⁺ i1⁻

Basia: tak

abcd: To znowu ja z pytaniem... Dlaczego w tym zadaniu nie liczono granicy f(t) dla t dazacego do +/− nieskończoności? https://www.zadania.info/d1/4775483

abcd: Znaczy nie dla t dazacego do +/− nieskonczonosci, tylko −1+ i 1−, czyli dla krancow dziedziny f(t)?

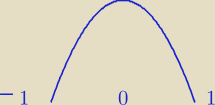
ite: W tym rozwiązaniu napisano: W takim razie pochodna jest dodatnia na przedziale ⟨− 1,0) i ujemna na przedziale (0 ,1), czyli funkcja y = f(t) rośnie w pierwszym z tych przedziałów i maleje w drugim. To oznacza, że ma w tym przedziale maksimum i pozostałe wartości są mniejsze od tej w maksimum. My szukamy największej wartości funkcji w tym akurat przedziale, a tu tutaj przebieg zmienności funkcji jest jednoznaczny. Jeśli masz wątpliwości, to możesz liczyć wartości f(−1) i f(1), może łatwiej będzie zobaczyć że to nie są wartości największe.

ite: i jeszcze jedna uwaga : funkcja wartości f(t) jest określona dla t=1 i t=−1 i jest w nich ciągła, dlatego liczymy wartości f(−1) i f(1) a nie granice

abcd: czyli policzenie f(−1) i f(1) i porównanie z maksimum lokalnym nie byłoby błędem?

iteRacj@: byłoby niepotrzebne, widać że nie ma takiej potrzeby ale punktów karnych pewnie za to nie dadzą

Basia: przecież tam zrobiono podstawienie t = cos x y=cos x przyjmuje wartości z ptzedziału <−1;1> więc t również

Basia: czyli dziedziną funkcji f(t) jest <−1;1>