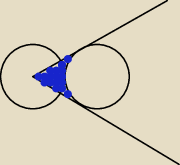
Dwa okręgi o równych promieniach są styczne zewnętrznie. Ze środka jednego z nich poprowadzono
styczne do drugiego okręgu (rysunek). Wykaż, że pole koła ograniczonego każdym z tych okręgów
| 3Pπ | ||
jest równe | , gdzie P jest polem zacieniowanej figury | |
| 3√3−π |
| 3√3−π | ||
pole tej zacieniowanej figury juz obliczylem, ale nie wiem co dalej P= | *r2 | |
| 3 |
| 3Pπ | ||
πr2 = | ||
| 3√3−π |
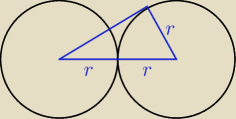
| P | (2r)2√3 | πr2 | |||
= | − | ||||
| 2 | 2*4 | 6 |
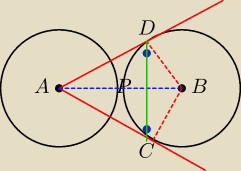AB=2R
BC=BD=R
AD2 = (2R)2−R2 = 3R2
AD = AV = R√3
wynika z tego, że kąt BAD = kąt BAC = 30
czyli tr.CAD jest równoboczny
| (R√3)2√3 | 3R2√3 | |||
PACD = | = | |||
| 4 | 4 |
| 120 | πR2 | |||
Pwycinka PCBD = | *πR2 = | |||
| 360 | 3 |
| πR2 | 1 | πR2 | R2√3 | ||||
− | *R*R*sin(120) = | − | |||||
| 3 | 2 | 3 | 4 |
| 3R2√3 | πR2 | R2√3 | ||||
P = PACD − Podcinka = | − | + | = | |||
| 4 | 3 | 4 |
| πR2 | ||
R2√3 − | ||
| 3 |
| π | 3√3−π | |||
P = R2(√3− | ) = R2* | |||
| 3 | 3 |
| 3P | ||
R2 = | ||
| 3√3−π |
| 3Pπ | ||
Pkoła = πR2 = | ||
| 3√3−π |
w sumie to bylo proste
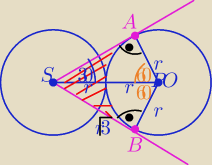W trójkącie "ekierce" : |OS|=2r , |OA|=OB|=r , |BS|=AS|=r√3
| 1 | ||
P(AOBS)=2* | r*r√3= r2√3 | |
| 2 |
| 120 | 1 | |||
P(wycinkaAOB)= | πr2= | πr2 | ||
| 360 | 3 |
| πr2 | r2 | |||
P(ASB)=P= r2√3= | = | (3√3−π) | ||
| 3 | 3 |
| 3P | ||
to r2= | ||
| 3√3−π |
| 3Pπ | ||
P(koła) = | ||
| 3√3−π |
I jeszcze korekta zapisu
| πr2 | r2 | |||
P(ASB)=P=r2√3− | = | (3√3−π) | ||
| 3 | 3 |