na prostej julia: Na prostej zaznaczono pewną liczbę punktów, a następnie każde dwa z tych punktów połączono odcinkiem. Jeden spośród zaznaczonych punktów leży dokładnie wewnątrz 80 narysowanych odcinków, a inny dokładnie wewnątrz 90 odcinków (punkt leży wewnątrz odcinka, gdy leży na odcinku, ale nie jest jego końcem). Ile punktów zaznaczono na prostej? (do wyboru 20, 22, 80, 90)

stevve: a nie 92 czasem?

julia: nie, 80 i 90

stevve: to nie wiem

Basia: moim zdaniem 20 punktów zupełnie wystarczy

Basia: po lewej punkty A₁,A₂,....,A₁₀ po prawej B₁,B₂,....,B₁₀ czerwony należy do A₁B₁,.....A₁B₁₀ czyli 10 A₂B₁, A₂B₁₀ czyli 10 i tak dalej czyli należy do każdego odcinka A_iB_j i,j=1,2,..,10 czyli należy do 100 odcinków P=A₁ to nie należy do A₁B_j gdzie j=1,....,10 czyli nie należy do 10 z nich czyli należy do 90 Q=A₂ nie należy do tych co wyżej i do żadnego postaci A₂B_j czyli jeszcze do 10 czyli należy do 80 ale nie wykluczam, że jeszcze czegoś nie widzę

Pytający: 22 n // szukana liczba punktów l₁, p₁ // punkty "na lewo" i "na prawo" od pierwszego punktu z treści l₂, p₂ // punkty "na lewo" i "na prawo" od drugiego punktu z treści

⎧	l1p1=80
⎜	l1+p1+1=n
⎨	l2p2=90
⎩	l2+p2+1=n

⇒

	80		90
n−1=l1+		=l2+
	l1		l2

Wystarczy podstawiać kolejne dzielniki 80 jako l₁, jedynie dla l₁=16 otrzymujemy pasującą do

	80
odpowiedzi wartość: n−1=16+		=21 (więc pasuje do odpowiedzi n=22), sprawdzamy dla
	16

	90
drugiego punktu i faktycznie dla l2=15 otrzymujemy n−1=15+		=21. Stąd n=22.
	15

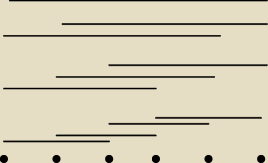
piotr: 90