Geometria analityczna Kasia: W trapezie równoramiennym ABCD przekątna AC jest dwusieczną kąta ostrego przy dłuższej podstawie AB. Podstawa AB zawiera się w prostej o równaniu y=−4, zaś ramię AD w prostej o równaniu y=√3x−2. Obilcz długość boków trapezu, wiedząc że jego pole jest równe 9√3. Nakierowalby ktos jak to zacząć i poprowadzic do konca?

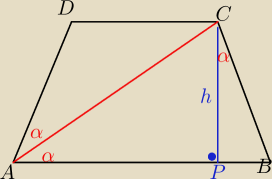
Basia: prosta y=−4 || OX kąt nacylenia ramienia AD do podstawy AB jest taki jak kąt nachylenia prostej y=√3x−2 do osi OX tg(kąta A) = √3 ⇒ |kąta A| = 60 α=30 AC = 2h AP = h√3 BC =2PB h = PB√3

	h
PB =
	√3

	h		3h+h		4h
AB = AP+PB = h√3+		=		=
	√3		√3		√3

	4h		2h		2h
CD = AB − 2PB =		−		=
	√3		√3		√3

	1		4h		2h
P =		(		+		)*h
	2		√3		√3

1
	*6h√3*h = 9√3
2

3h²√3 = 9√3 h² = 3 h=√3 reszta to już tylko podstawienie do powyliczanych zależności sprawdź czy się tam gdzieś w rachunkach nie pomyliłam

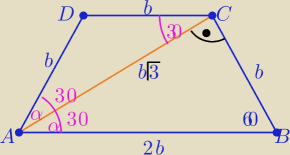
Eta: Współczynnik kierunkowy prostej AD a=√3 i AB: y= −4 to kąt między prostymi AD i AB jest 2α to tg(2α)=√3 ⇒ 2α=60^o pozostałe oznaczenia na rysunku P(trapezu) = P(ADC) +P(ABC)

1		1
	b*b*sin120o+		*b√3*b = 9√3
2		2

..................... zatem 3b²=36 ⇒ b= 2√3 to boki trapezu mają długości 2√3, 2√3, 2√3,4√3 ≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈