RACHUNEK RÓŻNICZKOWY bluee: Rozważmy wszystkie stożki o tworzącej l. Uzasadnij, że największą objętość ma stożek, o

	√3
wysokości równej h=		l.
	3

bluee: H²+r²=l² H=√l²−r²

	1
V=		πr2H
	3

	1
V=		πr2H√l2−r2
	3

Nie wiem, jak pozbyć się niewiadomej r.

Mila:

	1
V=		πr2*H
	3

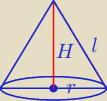
l²=r²+H² r²=l²−H²

	1
V(H)=		π*(l2−H2)*H
	3

	1
V'(H)=		π*(l2*H−H3)
	3

	1
V'(H)=		π*(l2−3H2)
	3

V'(H)=0⇔l²−3H²=0 3H²=l²

	l2
H2=
	3

	l		√3
H=		=		*l
	√3		3

l²−3H²>0

	l
H∊(0,		)
	√3

	l
Dla H=		funkcja V(H) ma największą wartość
	√3

bluee:

	1
Czy nie powinno być przypadkiem V'(H)=		π(2l−3H2)
	3

Basia: nie; pochodna jest "po H"; l jest tutaj zadaną wartością stałą

bluee: Sprawdziłam jednak Mila musi mieć rację, bo inaczej nie wychodzi wynik. Jednak czy pochodna z funkcji xⁿ nie wynosi nxⁿ⁻¹

bluee: No tak dzięki Basia

Basia: tak; (xⁿ)' = n*xⁿ⁻¹