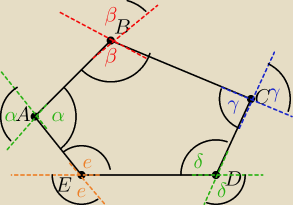
Kąty ostre wielokat Krzysiek60: Ile co najwyzej kątow ostrych moze miec dowolny wielokat wypukly W odpowiezi mam 3 kąty ostre i zajac sie katami zewnetrzymi wielokata Narysowalem sobie pieciokat wypukly α Suma katow zewnetrznych przy wierzcholku A= 2(180−α)= 360−2α wierzchoku B = 2(180−β)= 360−2β wierzcholku C= 2(180−γ= 360−2γ wierzchoklu D= 2(180−δ) = 360−2δ wierzcholku E= 2(180−e)= 360−2e jesli dodam te katy to mam 1800^o−2α−2β −2γ−2δ−2e I na tym stanalem

Krzysiek60:

iteRacj@: w dowolnym wielokącie wypukłym suma miar kątów zewnętrznych jest stała i wynosi 720^o podrawiam

Basia: kwadrat nie jest więc wielokątem wypukłym, bo 4*270 ≠ 720

Krzysiek60: Dobry wieczor i pozdrawiam Dobrze iteRacjo tylko jaki z tego jest wniosek

annabb: Suma kątów wewnętrznych to (n−2)*180

iteRacj@: Basia zaraz sprawdzam, ale chyba inaczej definiujemy kąt zewnętrzny wielokąta

Basia: suma kątów wewnętrznych w wielokącie wypukłym = (n−2)*180 k kątów ostrych; ich suma jest < 90*k zostało więcej niż (n−2)*180 − 90k i musisz to podzielić na n−k tak aby

(n−2)*180−90k
	< 180
n−k

(n−2)*180 − 90k < 180(n−k) 180n − 360 − 90k < 180n − 180k 90k < 360 k<4 tak mi się wydaje

iteRacj@: wg mnie to jest kąt wielokąta wypukłego, jeśli się mylę, to mnie poprawcie http://strefamatematyczna.uwm.edu.pl/wamat/licea/definicje/def_13_01_005_pg.pdf

iteRacj@: * kąt zewnętrzny wielokąta wypukłego jest taki jak tutaj

Krzysiek60: tak samo rozumuje iteRacjo z tymi katami . dzieki za rozpisanie Basiu

Basia: faktycznie iteRacja@ inaczej; przy takiej definicji to prawda

Basia: można też tak: suma dwóch kątów zwnętrznych danego kąta = 360−2α jeżeli 0<α<90 ⇒ 360−2α>180 720:180 = 4 czyli w tych 720 kątów większych od 180 mogę "upchnąć" co najwyżej 3

iteRacj@: jaki krótki i przejrzysty sposób, zupełnie nie wiedziałam, co zrobić z tymi kątami zewnętrznymi

Basia: