zad adam: 2log₅(2+√x)=log₃x rozwiaz nierownosc

adam: równanie

adam: pomocy

Krzysiek60: Moze zamien log₃x na logarytm przy podstawie z 5

PW: Widzę rozwiązanie: x=3², bo 2log₅(2+√3²= 2log₅5=2 i lo₃3²=2. Już jakiś punkcik za zadanie dostaniesz.Drugi za określenie dziedziny. Ciekawe, czy jest więcej rozwiązań.

Eta: Zamiana na logarytm dziesiętny

2log(2+√x)		logx
	=
log5		log3

logx*log5=2log3*log(2+√x) logx=2log3 lub log5=log(2+√x) x=9 lub √x+2=5 ⇒ x=9 ====== ======

adam: czemu logx=2log3 lub log5=log(2+√x)?

adam: to nie wynika z logx*log5=2log3*log(2+√x)

adam: pomocy

aniabb: skoro a•x=y•b to albo x=a albo y=b nie może być a=b bo je znamy

Eta:

adam : Nie rozumiem z czego to wynika tego w szkole nam nie mówili... musze

adam : log5≠2log3 to jak mozna to logx=2log3 lub log5=log (2+√x)

Basia: 5x = 7y z tego naprawdę nie wynika, że x=7 i y=5 chyba, że zażądamy aby x,y były całkowite a mimo to rozwiązanie jest prawidłowe

aniabb: można jeszcze tę dwójkę turlać .. ale pewnie wyjdą wtedy sprzeczne

Basia:

	1
log5(2+√x) =		log3x
	2

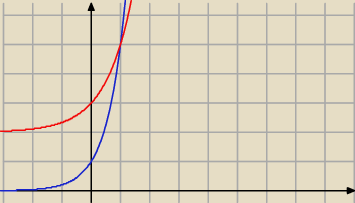
log₅(2+√x) = log₃x^1/2 log₅(2+√x) = log₃√x = t 5^t=2+√x 3^t = √x 5^t = 2+3^t rysujemy wykresy funkcji: y = 5^t y = 3^t+2 jedynym punktem wspólnym tych wykresów jest punkt (1,5) stąd t=1 log₃√x = 1 √x = 3¹=3 x=9

PW: I o to pytałem o 17:04. Chyba zgodzimy się, że Basia podała sposób rozwiązania dostępny dla ucznia, i wystarczający

Eta: