Przeksztalcenia izometryczne na plaszczyznie Krzysiek60: Dany jest trapez ABCD Okreslic wzajemnie jednoznaczne przeksztalcenie jednej podstawy trapezu na druga

PW: Na przykład jednokładność o środku M, gdzie M oznacza wspólny punkt przekątnych trapezu. Ale tym razem hasło "Przekształcenia izometryczne" to podpucha.

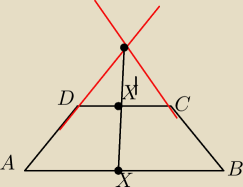
Krzysiek60: A mozna troche jasniej z ta jednokladnoscia ? W zbiorze zadan mam tak Przedluzmy ramiona trapezu do przeciecia sie w punkcie P i poprowadzmy przez ten punkt pek prostych Przyporzadkujmy wzajemnie punkty X i X' obu podstaw lezace na tej samen prostej peku tak okreslone przeksztalcenie jest wzajemnie jednoznaczne . Dlaczgo ? to pytam ja Bo jesli puntowi X na podstawie AB przyporzadkujemy punkt X' ba podstawie CD jka zrobimy odwrotne przeksztalcenie wokol punktu P? dalej jest oczwywiscie nie jest to jedyne przeksztalcenie wzajemnie jednoznaczne .

PW: To przekształcenie też jest jednokładnością, co wynika z twierdzenia Talesa. Być może zadanie jest z takiego etapu edukacji, na którym uczeń jeszcze nie zna tego twierdzenia, wtedy nie trzeba tego nazywać jednokładnością − wystarczy opis. Dowolnemu punktowi X przyporządkowujemy punkt X' w sposób pokazany na rysunku. Jest to przekształcenie wzjemnie jednoznaczne, gdyż prosta przecina każdy odcinek tylko w jednym punkcie. Każdy punkt X z podstawy AB ma więc dokładnie jeden obraz X' w podstawie BC, i odwrotnie. Także wzajemnie jednoznacznie przyporządkujemy punkty jednej podstawy punktom drugiej, gdy od X poprowadzimy prostą przez M − wspólny punkt przekątnych. Też to będzie jednokładność, ale o innym stosunku, w tym zadaniu nie trzeba go wyznaczać. Ważne, że każdy X będzie miał w ten sposób dokładnie jeden obraz X' i odwrotnie.

Krzysiek60: Jezu a ja sie uparlem przy symetrii osiowej tak jak w okregu . Robie sobie taki przerywnik zeby nie zwariowac przy trojkatach przystajacych Dziekuje PW