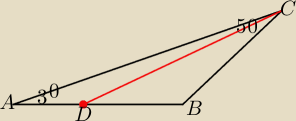
Trojkaty przystajace Dobra kawa: dany jest trojkat ABC w ktorym kątA= 30^o i kąt C= 50^o Punkt D lezy na boku AB przy czym BD= BC Wykazac ze CD= AB

Dobra kawa:

Krzysiek60:

PW: CD²=BC²+BD²−2BC^.DBcos100° Z założenia DB=BC, a więc CD²=2BC²−2BC²cos100° (1) CD²=2BC²(1−cos100°)

	BC		AB
		=
	sin30°		sin50°

	AB
2BC=
	sin50°

	AB2
4BC2=
	sin250°

	AB2
(2) 2BC2=		.
	2sin250°

Mam wrażenie, że podstawienie (2) w (1) da tezę.

Krzysiek60: Dziekuje Ci PW . Twoje rozwiazanie juz rano przeananlizuje . mam jednak znalezc trojkaty przystajace Wiec bede mial dwa rozwiazania .

PW: Ten temat "trójkąty przystające" to dla zmylenia przeciwnika. Ja widzę tw. kosinusów i tw. sinusów. Jeżeli ktoś potrafi coś dorysować, coś zaczarować i zobaczyć trójkąty przystające, to chcę to zobaczyć.

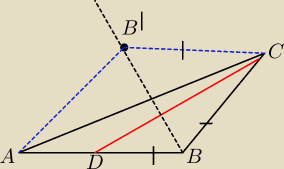
Krzysiek60: Dzien dobry PW Znalazlem takie rozwiazanie Oznaczmy przez B' punkt symetryczny do do wierzcholka B wzgledem prostej AC Wtedy kat BAB'= 2*30^o= 60^o oraz AB= AB' stad wynika z etrojkat BAB' jest rownoboczny Ponadto BD= BC= CB' oraz kat B"CB= 2*50= 100= 180−30−50= kat CBD wobec tego ΔB'CB przystaje do Δ CBD cecha BKB stad CD= B'B= AB

Krzysiek60: Powiem szczerze ze nigdy bym na to nie wpadl

PW: No i zaczarowali. dziękuję. Ze smutkiem stwierdzam, że poradziłem sobie jak rzemieślnik, wyliczyłem zamiast udowodnić. Jest to przykład na zjawisko "nadmiar wiedzy czasem przeszkadza". Ponieważ "widziałem" możliwość zastosowania twierdzeń, ten sposób wydał mi się oczywisty. Ktoś, kto nie zna tych twierdzeń, pomyśli i znajdzie.

Krzysiek60: Niestety nie potrafie dokonczyc tych obliczen jedynie co moge zapisac ze cos100^o= −sin10^o

	AB2
wiec CD2=		(1+sin10o}
	sin250o

	AB2		AB2*sin10o
CD2=		+
	sin250o		sin250o

PW: Wzór połówkowy dla cos100°. W związku z tym mam pytanie: − Czy w zadaniu jest istotne, że 100° i 50°, czy wystarczy ∡B=2∡C?

Krzysiek60: Nie potrafie tego roztrzygnac

PW:

	1
Nie wystarczy, bo w wyliczeniu korzystaliśmy z równości sin30°=		.
	2

Krzysiek60: Jesli bvys mogl w miedzyczasie dokonczyc te obliczenia to bylbym wdzieczny Naprawde nie wiem jak .

PW: (1) CD²=2BC²(1−cos100°) (1') CD²=2BC²(2sin²50°) i podstawić (2) do (1').