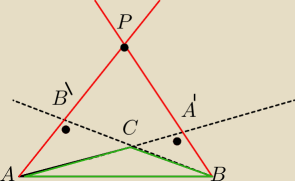
Trojkat rownoramienny Dobra kawa: W trojkacie ABC poprowadzono wysokosci AA' iBB' Proste zawierajace te wysokosci przecinaja sie w punkcie P Udowodnij ze jesli AP= PB to trojkat jest rownoramienny Prosze o pomoc w rozpatrzeniu przypadku gdy trojkat ABC jest rozwartokatny wtedy wysokosci przecinaja sie na zewnatrz trojkata Jednak mam pytanie na poczatek Czy dobrze narysowalem te dwie wysokosci bo z nimi mialem najwiekszy kolpot ? Na przyklad wysokosc AA' . Przedluzam ramie AC i z puktu B rysuje prosta prostopadle do tego przedluzenia Punkt przeciecia sie obydwu prostych wyznaczy punkt A"

Janek191: Wysokościami są: BA' i AB'

Dobra kawa: Tak ja rozumiem bo to trojkat rozwartokatny ale czy ich konstrukcja jest prawidlowa ?

Mila: Tak.

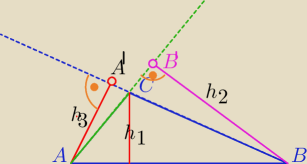
Mila: Masz wysokości ( bez przedłużeń).

Dobra kawa: To dalej AP= PB wiec trojkat ABP jest rownoramienny kąty przy podstawie tego trojkata sa rowne w trojkacie prostokatnym AB'B kąt B'BA = 90−α W trojkacie prostkatnym AA'B kat A'AB = 90−α Na podstawie cechy KBK ΔAB"B jest przystajacy do trojkata AA'B stad tak jak napisal Janek 191 BA'= AB' A to jest wlasnosc trojkata rownoramiennego

Dobra kawa: Dzieki Mila za rysunek i potwierdzenie