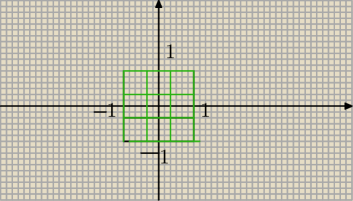
d bernio: potrzebuje pomyslu mam obszar [−1,1]² te kwadraty są ponumerowane, od lewej górnej to 1, po prawej 2, i ostatni w pierwszym rzędzie 3, później 4 itd... te kwadraty mają takie same długosci boków. nie mam pomyslu na rozwiazanie tego zadania, np. dostaje jakiś punkt, powiedzmy (0.87,0.25), mam powiedzieć w którym kwadracie jest ten punkt wskazać, dostane kilka takich punktów, jak do tego matematycznie podejść? mam napisać programik do tego, ale zastanawiam się jak to zrobić

bernio: podsunie ktoś pomysł

Blee: długość boku wyjściowego kwadratu to 2

	2
więc każdy z tych mały kwadratów ma bok długości
	3

otrzymujesz punkt o współrzędnych P(x,y) Jak szybko zobaczyć w którym kwadracie jest? Otóż

	1
x −		< 0 to odpadają kwadraty 3;6;9
	3

	1
x +		> 0 to odpadają kwadraty 1;4;7
	3

po tych dwóch operacja już wiemy w której 'trójce' znajduje się tenże punkt, wystarczy teraz analogicznie zrobić z y:

	1
y −		< 0 to odpadają kwadraty 1;2;3
	3

	1
y +		> 0 to odpadają kwadraty 7;8;9
	3

w efekcie mamy wyznaczony kwadrat w którym znajduje się tenże punkt

Blee: więc punkt (0.87 ; 0.25) mamy: 0.87 − 0.(3) > 0.5 > 0 <−−− czyli kwadraty 3,6,9 jedynie wchodzą w grę sprawdzamy po 'y': 0.25 − 0.(3) < 0 <−−− więc na pewno nie 3 0.25 + 0.(3) > 0.5 > 0 <−−− czyli nie 9 czyli w kwadracie 6 (prawy środkowy). Koooniec

wmboczek: w zależności od realizacji operacji dzielenia modulo 3 skalujemy wsp do kwadratu 0−3x0−3 obliczamy reszy z dziel x i y przez 3 (jeśli trzeba zaokr w dół) xmod3+3ymod3+1=nr kwadratu

bernio: Blee, właśnie na to wpadłem przed dodaniem Twojego wpisu, ale bardzo dziękuje

bernio: blee, mój sposób trochę inny, bo liczyłem moduł z różnicy i sprawdzałem ile razy odejmie się 1/2 boku i czy miesci sie w zakresie. a jak Twoim sposobem sprawdzić dla reszty kombinacji dla innych kwadratow

bernio: "skalujemy wsp do kwadratu 0−3x0−3" boczek podaj przykład, rozwiń myśl

wmboczek: x*1,5+1,5 zamieni liczbę x∊ (−1;1) na liczbę z (0;3)

wmboczek: x*1,5+1,5 zamieni liczbę x∊ (−1;1) na liczbę z (0;3)

kochanus_niepospolitus: bernio −−− procedura jest taka sama za każdym razem. Zauważ, że dla tamtego punktu zrobione zostały 3 (z 4) kroków tylko ze względu na to, że po 'x' od razy wyszło że jest to gdzieś w 'prawych kwadratach'.

4bernio: Możesz rozwinąć kochanus bo nie rozumiem

4bernio: Wmboczek nie.rozumiem Twojego sposobu

kochanus_niepospolitus: Ale czego nie rozumiesz ? Konkretnie. Najlepiej to sobie 'przetestuj' obie metody na paru wylosowanych punktach to szybko zrozumiesz jak działają ów metody

bernio: mam 9 kwadratow 1)sprawdzam dla x x−1/3 < 0 − odpadają kwadraty 3;6;9 skoro tutaj jest prawda, to warunek x+13 > 0 jest falszywy więc zostają mi 1;4;7 2) teraz sprawdzam dla y y−1/3 < 0 odpadają 1.2.3 y+1/3> 0 odp. 7.8.9 powiedzmy że y−1/3 < 0 to jest prawdą, więc drugi warunek jest fałszem, wiec odpadają 1.2.3<< 1 wykreślam (bo mam 1.4.7 z warunku dla x) zostają mi kwadraty 4.7 koniec warunków, który wybrać?

bernio: aj dobra, zerkne na to jeszcze raz, opacznie zrozumialem

bernio: kochanus, a co jeśli będzie punkt (0,98, 0,98) mógłbyś mi powiedzieć jak rozpisać ten przyklad?

bernio: 1)dla x 0,98 − 0,3 < 0 zostają 3,6,9 dla y 0.98+1/3>0 tak zostają 1,2,3 i część wspólną?

bernio: lub gdy będzie punkt (0.1, 0.1) to nic nie pasuje

4bernio:

bernio: ALE ZE MNIE KRETYN, WĄTEK ZAMYKAM XD sprawa rozw.

Blee: