wykaż radzio: Trapez o kątach ostrych 45⁰ i 30⁰ jest opisany na okręgu o promieniu r Wykaż że stosunek obwodu trapezu do średnicy tego okręgu jest równy 4+2√2

Blee: skoro czworokąt jest opisany na okręgu to: a+b = c+d (gdzie c,d to ramiona trapezu) więc Obw = 2*(c+d) średnica okręgu to nic innego jak wysokość trapezu (h) z funkcji trygonometrycznych:

	h
sin 45o =		−> c = √2h
	c

	h
sin30o =		−> d = 2h
	d

czyli :

Obw		2*(c+d)		2*(2h+√2h)
	=		=		= 4+2√2
h		h		h

c.n.w.

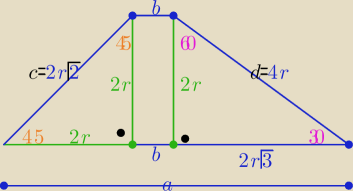
Eta: 1/ h=2r −−− dł. średnicy okręgu wpisanego w trapez 2/ z trójkątów "ekierek" c= 2r√2 i d=4r 3/ z warunku wpisania okręgu w trapez : a+b= c+d ⇒ L(ABCD)=2*(c+d) = 2r(4+2√2)

	L
to :		= 4+2√2
	2r

≈≈≈≈≈≈≈≈≈≈ c.n.w

Eta: HejBlee "gary po obiedzie umyłeś"?

Blee: Niet Bo obiadu nie jadłem