dowód na przystawanie
emiliee123: Hej,mam takie zadanie i szczerze mówiąc nie wiem jak się do niego zabrać, a w czwartek czeka
mnie to na sprawdzianie i chciałabym przećwiczyć

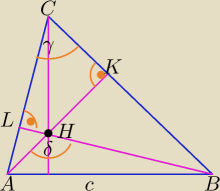
Punkt H jest punktem przecięcia się wysokości trójkąta ABC. Wykaż, że okręgi opisane na
trójkątach ABH, BCH i CAH są przystające
Mila:
1)
2)
∡LHK=180
o−γ z sumy kątów w czworokącie KHLC
3) W ΔABH :
| | c | | c | |
2r= |
| = |
| =2R⇔ |
| | sin(180−γ) | | sin(γ) | |
r=R
Analogicznie wykażesz w pozostałych Δ.
Promienie okręgów opisanych na trójkątach ABH, BCH i CAH
są równe promieniowi opisanemu na ΔABC.
 Punkt H jest punktem przecięcia się wysokości trójkąta ABC. Wykaż, że okręgi opisane na
trójkątach ABH, BCH i CAH są przystające
Punkt H jest punktem przecięcia się wysokości trójkąta ABC. Wykaż, że okręgi opisane na
trójkątach ABH, BCH i CAH są przystające
 1)
1)