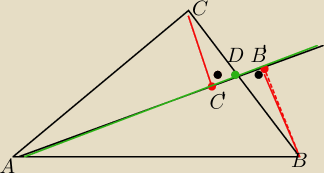
 W trojkacie ABC poprowadzono srodkowa AD
Udowodnij ze punkty B i C sa rowno oddalone od prostej AD
Czyli muszse wykazac ze CD= DB
Ale zeby to wykazac muszse wykazac ze ΔC'CD≡ΔDBB'
CC' − rzut prostokatny punktu C na prosta AD
BB' − rzut prostokatny punktu B na prosta AD
CD= DB z warunkow zadania
kąt CC"D= kątowi BB'D jako katy proste
kąt C'CD= katowi B'BD ( ale tutaj nie jestem do konca pewen
Na podstawie cechy KBK trojkaty te sa przystajace wiec CD= DB
W trojkacie ABC poprowadzono srodkowa AD
Udowodnij ze punkty B i C sa rowno oddalone od prostej AD
Czyli muszse wykazac ze CD= DB
Ale zeby to wykazac muszse wykazac ze ΔC'CD≡ΔDBB'
CC' − rzut prostokatny punktu C na prosta AD
BB' − rzut prostokatny punktu B na prosta AD
CD= DB z warunkow zadania
kąt CC"D= kątowi BB'D jako katy proste
kąt C'CD= katowi B'BD ( ale tutaj nie jestem do konca pewen
Na podstawie cechy KBK trojkaty te sa przystajace wiec CD= DB
 Zostawiam to na jutro Dobranoc
Zostawiam to na jutro Dobranoc 
| 1 | 1 | ||
*|AD|*|CC'|= | |AD|*|BB'|⇔ | ||
| 2 | 2 |
 Mam we wskazowce do zadania zeby rozpatrzyc trojkaty przystajace CDC"i BDB'
Wiec tak ja napisal Blee muszse wykazac ze BB'= CC'
Za twoje rozwiazanie dziekuje
Mam we wskazowce do zadania zeby rozpatrzyc trojkaty przystajace CDC"i BDB'
Wiec tak ja napisal Blee muszse wykazac ze BB'= CC'
Za twoje rozwiazanie dziekuje 