plis bąk: Wyznacz równanie okregu stycznego wewnetrznie do okregu o równaniu (x − 2)²+y²=4 i do prostej y = 0, którego ´srodek ma współrzedne róznych znaków i lezy na wykresie ˙ funkcji y = −x³+1/4

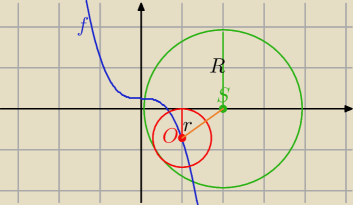
Eta: 1/ poglądowy rysunek: 2/ S(2,0), R=2 O(a,b) , r=|b| i a>0 , b<0 i O∊f(x) 3/ z warunku styczności wewnętrznej okręgów: |SO|²=|R−r| ⇒ (a−2)²+b²=(2−b)² ⇒ .................

	a−4a		a2−4a
b=		to O(a,		)
	4		4

	1		a2−4a
i O∊f(x) ⇒ −a3+		=		/*4
	4		4

−4a³+1=a²−4a⇒ 4a³+a²−4a−1=0 ⇒ a²(4a+1)−(4a+1)=0 (4a+1)(a²−1)=0 i a>0 ⇒ a=1

	1−4		3		3
to b=		= −		i r= |b|=
	4		4		4

	3		9
zatem o : ( x−1)2+(y+		)2=
	4		16

≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈