help dnsfhsn: Dany jest graniastosłup prawidłowy trójkatny ABCDEF o podstawach ABC i DEF, w któ− rym wszystkie krawedzie maja te sama długosc. Wykaz,˙ ze jezeli przekrój tego grania− ˙ stosłupa płaszczyzna zawierajaca krawedz podstawy AB jest trapezem, to płaszczyzna ta jest nachylona do płaszczyzny podstawy ABC tego graniastosłupa pod takim katem α, ze˙ tg α >2√3/3

Janek191: β

Blee:

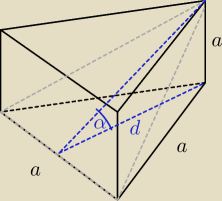
	a		a		2		2√3
tg α =		=		=		=
	d		a√3   2		√3		3

zauważ, że aby przekrój był trapezem to kąt musi być WIĘKSZY od wyznaczonego kąta α

	2√3
stąd (jako że tangens jest funkcją rosnącą ) tg α >
	3

c.n.w.

ssss: dzieki

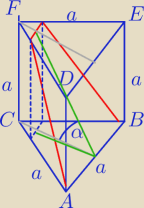
Janek191: β = I ∠ CKF I K − środek odcinka AB Mamy β < α < 90^o więc

	a		a		2		2 √3
tg β =		=		=		=
	h		√3   a   2		√3		3

więc

	2 √3
tg α > tg β =
	3

h − wysokość Δ równobocznego o bokach długości a.

ssss: dzieki