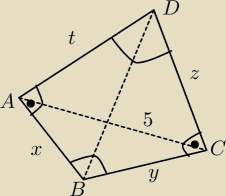
Ice Tea: Treść zadania: W czworokącie ABCD dane są: |AC| = 5 |∡BAD|=|∡BCD|=90, sin ∡ABC = ^√5₃. Oblicz długość przekątnej BD. (ten rysunek ja zrobiłem, nie ma go w treści zadania) Kąt ABC oznaczyłem jako α, a kąt ADC jako 180−α I teraz moje obliczenia: sin α = ^√5₃ cos α = ²₃ sin (180 − α) = ^√5₃ cos (180 − α) = −²₃ Musimy obliczyć |BD|: |BD|² = x²+t²=y²+z² = ? Z tw. cosinusów wyszło mi to: x²+y²−⁴₃xy −25=0 t²+z²+⁴₃tz − 25=0 I na tym się zatrzymałem i nie wiem co dalej

ol: Zobacz ze na nim można opisac okrąg i wtedy DB to srednica, wiec z tw sinusów 5/sinβ=2R

Janek191: To jest czworościan !

Ice Tea: Skąd wiesz że DB to średnica?

Blee: Janek ... jeżeli jest to na płaszczyźnie to nie jest Przerywane linie oznaczają przekątne

Janek191: Może być też czworokąt.

ol: okrag opisany na trójkacie prostokątnym?

Janek191: Podane kąty są proste, więc BD jest średnicą okręgu opisanego na ABCD.

Blee: Ice Tea −−− masz trójkąt PROSTOKĄTNY ABD ... na tym trójkącie opisujesz okrąg to srodek okręgu jest na przeciwprostokątnej czyli na BD Natomiast skąd wiemy, ze na tym czworokącie można opisać okrąg? Bo suma kątów przeciwległych = się sobie i = 180^o

Ice Tea: 5 / sinβ = 2R 5 / ^√5₃ = 2R 2R = 3√5 |DB| = 3√5 dobrze?