Wykres funkcji 1313: Jak naszkicować wykres |y| ≥ |x| ?

1313: Raczej zbiór rozwiazań tego ?

Jerzy: Rozpatrz 4 przypadki w zależności od znaku x i y

Blee: 1) y>0 rysujesz y ≥ |x| 2) y≤0 rysujesz −y≥ |x| ⇔ y ≤ |x|

1313: Dzięki!

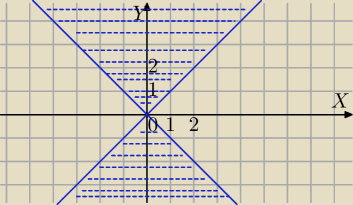
Mila: |y| ≥ |x| Blee zgubił minus. −y≥|x|⇔y≤−|x|

: ile to już razy było to samo

PW: ... a ciągle nie bardzo wiadomo, dlaczego taki rysunek. |y|≥|x| ⇔|y|²≥|x|² ⇔ y²≥x² ⇔ (y−x)(y+x)≥0 ⇔((y−x)≥0∧y+x)≥0)∨((y−x)≤0∧y+x)≤0) ⇔ iloczyn nieujemny − oba czynniki nieujemne lub oba niedodatnie ⇔ (y≥x ∧ y≥−x) ∨ (y≤x ∧ y≤−x) Pary (x,y) spełniające pierwszy układ nierówności to zbiór leżący nad osią OX zaznaczony przez \Milę, spełniające drugi układ − leżący pod osią OX, razem z prostymi.