Nieróność z pierwiastkiem Agata: Podaj największą liczbę całkowitą p spełniającą nierówność: p<√2p−2+1 1. Wyznaczam dziedzinę p≥1 2. rozpatruje dwa przypadki dla p>0 p<√2p−2+1 | ⁽2) 0<−p²+2p−1 Δ=0 p₀=1 oraz dla p<0 to jest poza dziedziną funkcji. Zatem czy największa liczba całkowita spełniająca nierówność to 2?

Blee: Przeciez dziedzina wyszla Ci p≥1 natomiast z pierwszego przypadku wyszlo p<1 ... stad wniosek

Blee: Druga sprawa − nieumiejetne podniesienie do kwadratu p < √2p − 2 + 1 p− 1 < √2p − 2 //² p² −2p +1 < 2p − 2 0 < −p² + 4p − 3 0 < −(p−3)(p−1)

Agata: hmm. nie istnieje p spełniające nierówność?

Agata: okej to już spróbuję to ogarnąc z prawidłowym kwadratem momencik

Blee: Odpowiedz mialas dobra, ale blednie (w niewyjasniony dla mnie sposob) do niego doszlas.

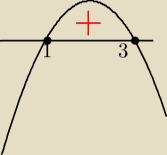
Agata: okej już mam tak nad osią (1,3) zatem największa całkowita spełniająca nierówność to 2

Blee: dokładnie

Blee: a teraz spójrz w jaki sposób wcześniej podniosłaś do kwadratu i zapamiętaj aby TAK NIE ROBIĆ

Agata: tak wiem coś mnie przyćmiło.. ale postaram się pamiętać BAARDZO dziękuje