Równanie: sześcian: Równanie: dla jakiej wartosci m rownanie nie ma rozwiazan :

	2		m+3
2+		=
	|x|−2		m

ja chciałem tak że :

2		3−m
	=
|x|−2		m

mnoze na krzyż i wychodzi że : |x|(3−m)−6=0 wiec dla m=3 by nie bylo , ale no nie zgadza sie, czemu tak nie moge i jak to zrobic ?

Basia: można tylko trzeba napisać założenia |x|−2≠0 x≠2 ∧ x≠ −2 ∧ m≠0 2m = (3−m)(|x|−2) 2m = (3−m)*|x| − 2(3−m) (3−m)*|x| = 2m+2(3−m) (3−m)*|x| = 6 dla m=3 nie ma rozwiązania dla m≠3

	6
x=
	3−m

6		6
	≠2 i		≠−2
3−m		3−m

6≠2(3−m) i 6≠−2(3−m) 6≠6−2m i 6≠ −6+2m 2m≠0 i 2m≠12 m≠0 i m≠6 równanie nie ma rozwiązania dla m=0, dla m=3 i dla m=6

sześcian: tyle ze w odp mam przedzial a nie konkretne liczby

sześcian: gdyby potraktowac lewa strone jako funckje i narysowac ta funkcje to wlasnie w sumie bylomy ze :

	m+3
1<		<2
	m

i nie wiem ktora interpetacja jest ok i dlaczego

Basia: a jaki masz ten przedział ?

Basia: oj też zrobiłam błąd; zgubiłam wartość bezwzlędną

Basia: jeszcze raz od początku

Basia:

	2		m+3
2+		=
	|x|−2		m

|x|≠2 i m≠0

2		m+3
	=		−2
|x|−2		m

2		m+3−2m
	=
|x|−2		m

2		3−m
	=
|x|−2		m

2m = (3−m)(|x|−2) 2m = (3−m)*|x| − 2(3−m) 2m = (3−m)*|x| − 6 + 2m (3−m)*|x| = 6 m = 3 0=6 sprzeczność czyli m≠3 dla m≠3 mamy

	6
|x|=
	3−m

6		6
	≥0 i		≠2
3−m		3−m

3−m>0 i 6≠2(3−m) m<3 i 6≠6−2m m<3 i m≠0 m∊(−∞,0)∪(0;3) taką masz odpowiedź czy inną ?

Basia:

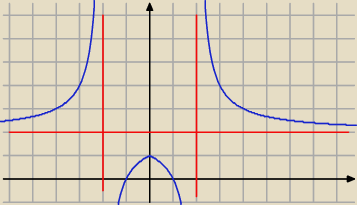
	2
to jest wykres Twojej funkcji y = 2+
	|x|−2

jej zbiór wartości to (−∞;1>∪(2;+∞) czyli musi być:

m+3		m+3
	<1 lub		>2
m		m

m+3		m+3
	−1<0 lub		−2>0
m		m

m+3−m		m+3−2m
	<0 lub		>0
m		m

3		3−m
	<0 lub		>0
m		m

m<0 lub m(3−m)>0 m<0 lub m∊(0,3) czyli ma rozwiązania dla m∊(−∞;0)∪(0;3) a nie ma dla m∊<0;3> obie interpretacje dają ten sam wynik; obie są poprawne

Basia: poprawka: a nie ma dla m∊{0}∪<3;+∞)

Basia: dokładniej nie ma dla m∊<3;+∞) dla m=0 równanie nie ma sensu