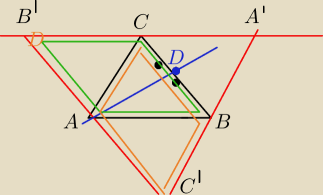
dowod Krzysiek60: Udowodnij z e proste zawierajace wysokosci dowolnego trojkata przecinaja sie w jednym punkcie Dowod Przez wierzcholki trojkata ABC prowadzimy proste rownolegle do przeciwleglych bokow Otrzymujemy trojkata A'B'C' Niech AD bedzie wysokoscia w trojkacie ABC czyli AD⊥B'C' Takze otrzymalismy dwa rownolegloboki AC'BC i B'A BC w ktorych AC'= BC BA'= BC Z tego wynika ze punkt A jest srodkiem boku B'C'w trojkacie A'B"C' Wobec tego prosta AD jest symetralna boku C'B' Tak samo wykazujemy ze proste zawierajace pozostale wysokosci troakt ABC sa symetralnymi bokow trojkata A'B"C' A symetralne w trojkacie przecinaja sie w jednym punkcie bo juz udowodniono . Moze jakis inny sposob na udowodnienie ze wysokosci w trojkacie przecinaja sie w jednym punkcie

Mila: https://pl.wikipedia.org/wiki/Wysoko%C5%9B%C4%87_tr%C3%B3jk%C4%85ta

Krzysiek60: Dziekuje Ci Milu Dobranoc