trygoma kaka: Może mi ktoś wyjaśnić? nie rozumiem za bardzo jak powstały te przekształcenia. Uczę się sama bez nauczyciela, mam tylko podstawę, wiec nie potrafię sama wszystkiego ogarnąć Wyznacz zbiór wartości funkcji f(x)=sinx+cosx f(x)=sinx+sin(^π₂−x) = 2sin^π₄cos(x−^π₄=√2cos(x−^π₄)

Basia:

	π
1. wzory redukcyjne sin(		−x) = cosx
	2

2. wzór na sumę sinusów

	x+y		x−y
sinx + siny = 2sin		*cos
	2		2

	π		√2
3. sin		=
	4		2

Adamm: tutaj skorzystali ze wzoru na sumę sinusów, ale ja wolę skorzystać ze wzoru na sumę kątów f(x)=sinx+cosx=√2(cos(π/4)sinx+sin(π/4)cosx)=√2sin(x+π/4)

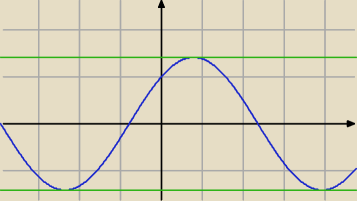
Janek191: cd.

	π
−1 ≤ cos( x −		) ≤ 1 / * √2
	4

	π
− √2 ≤ √2 cos ( x −		) ≤ √2
	4

więc ZW = < −√2 , √2 > ================

Mila: Korzystasz z wzorów ( Patrz do tablic) sin(90−α)=cosα, cos(90−α)=sinα

	x+y		x−y
sinx+siny=2*sin		*cos
	2		2

zbiór wartości:

	π
f(x)=√2*cos(x−		)
	4

	π
−1≤cos(x−		)≤1 /* √2 ⇔
	4

	π
−√2≤√2*cos(x−		)≤√2
	4

Zw_f=<−√2, √2>

kaka: Dzięki wielkie Jeśli mam zadanie na obliczenie sin ^2π₃*cos ^7π₆ − tg^11π₄* sin ^13π₄ To korzystam z tych samych wzorów co w tym poprzednim zadaniu?

Janek191: Pisz ułamki przy pomocy litery U

Janek191: Najlepiej zamień na stopnie

Adamm: nie ma sensu zapamiętywać tych wszystkich wzorów sin(x+y)=sinx*cosy+siny*cosx sin(x−y)=sinx*cosy−siny*cosx sin(x+y)+sin(x−y)=2sinx*cosy proste wyprowadzenie

kaka: Dziękuję wam bardzo

Basia: ad. post z 22:08

	2π		7π		11π		13π
sin		*cos		− tg		* sin		=
	3		6		4		4

	π		π		π		π
sin(π−		)*cos(π+		) − tg(3π−		)*sin(3π+		) =
	3		6		4		4

z okresowości

	π		π		π		π
sin(π−		)*cos(π+		) − tg(−		)*sin(π+		) =
	3		6		4		4

z wzorów redukcyjnych

	π		π		π		π
sin		*(−cos		) − (−tg		)*(−sin		) =
	3		6		4		4

	√3		√3		√2
−		*(−		)− 1*
	2		2		2

kaka: Dziękuję