Planimetria Ania: Planimetria Hej, właśnie wykonuję zadanie z planimetrii, w którym mam rozwiązać trójkąt o danych bokach i kącie: a = 10, c = 20,γ = 150° Licząc sinusa wyszło mi, że Sin = 1/4, chciałam się upewnić czy idę dobrym tokiem Sin = 1/4 = 0,25 ≈ 14° ?

Basia:

dziadek: 1/4 ≈ 14^o co to za bełkot

dziadek: sin150^o = sin30^o = 1/2

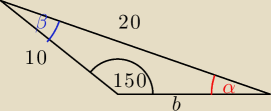
Michał: Cześć Ania, podstawą każdego (no może tylko większości) zadań z planimetrii jest rysunek. Korzystamy z twierdzenia sinusów. No i jeszcze może się przydać:

	1
sin(150) = sin(180−30) = sin(30) =
	2

20		10		1
	=		−−−> sinα =
sin150		sinα		4

To masz dobrze, kontynuuj.

Basia: skrót myślowy; Ania miała na mysli, że α≈14^o

Ania: Okej, dziękuję wszystkim za liczne i szybkie odpowiedzi. Pozdrawiam

PW: Ta wypowiedź jest mało zrozumiała: Licząc sinusa wyszło mi, że Sin = 1/4, chciałam się upewnić czy idę dobrym tokiem Sin = 1/4 = 0,25 ≈ 14° ? Domyślam się, że stosując twierdzenie sinusów wyliczyłaś,

	1
sinα=
	4

− i dobrze, ale na tym koniec. Nie można stosować przybliżonych wartości kątów.

Basia: można PW, tak teraz uczą

Ania: @PW rozwiązując trójkąt muszę obliczyć α, β i γ.

	1
Tak jak napisał Pan Michał wynik α =		, γ = 150, z tego co uczą w szkole powinnam
	4

sprawdzić

	1
ile wynosi Sin α =		i następnie wyliczyć ostatni kąt. Z góry przepraszam, jeśli piszę tu
	4

coś źle ale po, to właśnie założyłam ten temat aby upewnić się czy nie popełniam błędu.

Basia: nie wiem na jakim jesteś etapie; można nie odczytywać tego kąta α w przybliżeniu

	1
tylko poprzestać na tym, że sin α =
	4

następnie policzyć sin β = sin(180−(α+γ)) = sin(α+γ) = sin(α)*cos(γ)+sin(γ)*cos(α) (cosinusy z jedynki trygonometrycznej) bok b z tw.sinusów

PW: Bok b można też obliczyć z twierdzenia kosinusów: c²=a²+b²−2abcosγ

	√3
400=100+b2−20b(−		)
	2

b²+10√3b−300=0 Δ=300+1200=1500, √Δ=10√15,

	−10√3+10√15
b=		=5√3√5−5√3=5√3(√5−1).
	2

Brzydkie, ale dalej dokładnie

	b		a
		=
	sinβ		sinα

	bsinα
sinβ=
	a

	1   5√3(√5−1)   4
sinβ=
	10

	√3(√5−1)
sinβ=
	8

Teraz można liczyć przybliżoną wartość kąta β (ok.15°30'), tak jak przybliżona wartość α to 14°30'.

Bogdan:

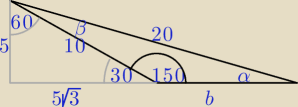
	1
Moja propozycja: sin150o =
	2

	20		10		1
Z tw. sinusów:		=		⇒ sinα =
	sin150o		sinα		4

Z tw. Pitagorasa: (b + 5√3)² = 400 − 25 ⇒ (b + 5√3)² = 25*15 b + 5√3 = −5√15 sprzeczność lub b + 5√3 = 5√15 ⇒ b = 5√15 − 5√3

	5√15 − 5√3		20		√15 − √3
Z tw. sinusów:		=		⇒ sinβ =
	sinβ		sin150o		8

PW: Szybciej z tym sprytnym dorysowaniem. A wiesz, że zaglądają tu takie adeptki, które twierdzą, że "w zadaniu otwartym nie można sobie tak dorysowywać"?

Bogdan: Ciekawe czego są to adeptki?