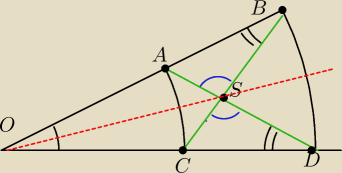
Dwusieczna kąta Krzysiek60: Na jednym ramieniu kąta α(α<180^o ) o wierzcholku O wybrano punkty A i B a na drugim punkty C i D tak ze AA= OC i OB= OD Proste AD i BC przecinaja sie w punkcie S Udowodnij ze polprosta OS jest dwusieczna kąta α Tak mysle ze nalezy udowodnic ze ΔASB≡CSD Z tresci zadania jest AB= DC OB= OD i OA=0C stad ∡OBC= ∡ODA ∡ASB=∡CSD jako wierzcholkowe Z rownosci tych na podstawie cechy KBK ΔASB≡ΔCSD wobec tego AS= CS Z tego OS jest dwusieczna kąta α

Krzysiek60: Moze byc ? A jakies inne podejscie do tego ?

Krzysiek60:

Basia: tr.ASB i CSD są przystające, więc ich wysokości wyprowadzone z S są sobie równe, a to są odległości S od ramion kąta z tego wynika, że S należy do dwusiecznej

Krzysiek60: A widzisz mozna Mozna

Basia: a skąd wziąłeś równość kątów B i D (tych zaznaczonych) ? to prawda, są równe, ale z czego to wynika ?

Krzysiek60: Basiu tak jak napisalem z rownosci tych odcinkow .

Krzysiek60: Czy to za mało ?

Basia: a tak już doczytałam

Basia: jest w porządku, przegapiłam uzasadnienie

Krzysiek60: OK