Przekształcenie funkcji 1313: Hej, mam problem z zadaniem dot. przekształceń funkcji. Mianowicie jest podany wykres funkcji f(x) i trzeba naszkicować wykres funkcji h(x)=f(1−|x|). Ja zrobiłam to w ten sposób: 1) dla x<0 bedzie h(x)=f(1+x) czyli przesuniecie o wektor [−1,0] 2) dla x≥0 bedzie h(x)=f(1−x) czyli po kolei: f(x) −− przesunięcie o wektor [−1,0] −−> f(x+1) −− odbicie względem OY −−> f(−x+1)=f(1−x) Ale mi to nie wychodzi i nie wiem co robie źle Z góry bardzo dziekuje za wyjaśnienie

Basia: jeżeli f(x+1) odbijasz symetrycznie względem OY dostajesz f(−(x+1)) = f(−x−1) podaj wzór funkcji f albo narysuj wykres; łatwiej będzie pokazać jak powinno być

1313: Właśnie też tak sądziłam ale jak ostatnio robiłam przekształcenia funkcji to w dwóch przypadkach tak to zrobiłam i wyszło jak miało być Próbowałam ją nnarysować ale nie wyszło ale opisze ja jak wyglada

1313: Od −∞ do −6 jest stala na −1 Od punktu (−6,−1) maleje do (−4,−3) Od (−4,−3) rosnie do (−1,3) Od (−1,3) do (4,3) jest stala I potem od (4,3) maleje przechodzac przez (5,0)

Mila: 1) Wykres f(x) 2) Symetria względem OY ⇒ wykres f(−x) 3) Przesunięcie o wektor [1,0]⇒ wykres f(−(x−1))=f(1−x) 4)Jeszcze raz symetria względem OY tylko tej części z prawej strony OY, obie części są wykresem f(1−|x|) Po kolacji narysuję przykładową funkcję.

1313: Oki dziękuje i smacznego

1313: Zrobiłam to w taki sposób i jest dobrze!

Basia: żeby dostać h(x) dla x≥0 trzeba najpierw wykonać symetrię względem OY a potem przesunąć o wektor [1;0] wtedy będzie dobrze np. h(0)=f(1) h(1) =f(0) h(4)=f(−3) h(5) = f(−4); h(7) = f(−6) itd. albo najpierw przesunąć o wektor [−1;0] a potem wykonać symetrię względem OY

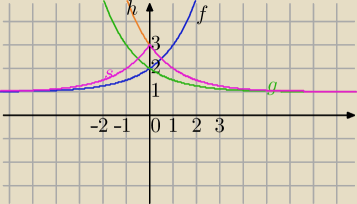
Mila: 1) f(x)=2^x+1 2) S_OY⇒[Z[g(x)=f(−x)]=2^−x+1] 3) T_[1,0]⇒h(x)=f(1−x)=2^1−x+1 4)S_{OY wykresu dla x≥0}⇒s(x)=2^1−|x|+1

1313: Basia: ja właśnie robiłam na początku tak jak Ty mówisz ale mi to nie wychodzilo powinno być wtedy tak jakby jeszcze jedna jednostke w prawo Nie wiem może nie powinnam rozbijać tego na dwa przypadki..

Basia: musiałeś się pomylić, bo jest dobrze; popatrz: h(7)=f(1−7) = f(−6) jeżeli zrobisz najpierw symetrię względem OY będzie (−6,−1)→(6,−1) przesunięcie [1;0] (6,−1)→(7,−1) i tak dalej, ale faktycznie lepiej nie rozbijać na dwa przypadki, bo zaczyna się mieszać

1313: Ale −6 jest mniejsze od zera czyli akurat dla tego punktu przesuniecie o jeden w lewo. A np dla (4,3) odbicie OY dostane (−4,3) potem [1,0] to będzie (−3,3) a powinno być (−2,3). Albo czegoś nie rozumiem

Basia: ale to miało działać tylko dla dodatnich; myślalam, że o to Ci chodzi w takim razie nieporozumienie