Styczne do krzywej :l: Pod jakim kątem przecinają się krzywe y=sinx i y=cosx? wskazówki

Jerzy: Pod takim samym jak styczne do nich w punkcie przecięcia.

Janek191: Oblicz miarę kąta między stycznymi do wykresów tych funkcji w punkcie ich przecięcia.

Basia: najpierw wyznacz punkty przecięcia, czyli równanie sin x = cos x potem liczysz pochodne i ich wartość w punkcie przecięcia tgα=f'(x₀) tgβ=g'(x₀) szukany kąt to |α−β|

:l: No tak wyznaczyłem punkt przecięcia w ten sposób. sinx=cosx sinx−cosx=0

	π
sinx−sin(		−x)=0
	2

... doszedłem do momentu

	π
x=		+kπ
	4

	√2
czyli punkt P(π/4,		)
	2

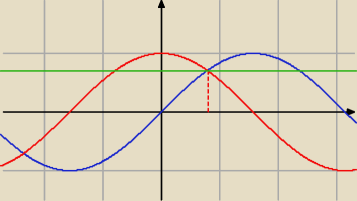
Janek191: Tak

:l: f'(x₀)=cosx₀ g'(x₀)=−sinx₀

	√2
f'(π/4)=
	2

	√2
g'(π/4)=−
	2

Jak policzyć

	√2
tgα=
	2

	√2
tgβ=−
	2

i dlaczego odejmujemy |α−β|

:l: W odpowiedzi mam tgγ=2√2

:l: Może policzyć styczną y₁ do sinx i y₂ do cosx tak jak napisał Jerzy

Janek191:

	π
a = cos		= 0,5 √2
	4

	π
a1 = − sin		= − 0, 5√2
	4

	0,5 √2 − ( −0,5√2)		√2
tg α =		=		= 2√2
	1 − 0,5√2*0,5√2		1 − 0,5

Basia:

	√2
tg α=
	2

	√2
tg β= −
	2

z tego wynika, że β>α nie są to wartości, z których dokładnie odczytamy kąty więc gdyby się dało policzylibyśmy po prostu β−α = |α−β| ( w tym wypadku ) liczymy tg(β−α) wg wzoru

:l:

	tgx−tgy
Rozumiem, ze skorzystałeś ze wzoru tg(x−y)=
	1+tgx*tgy

jasne, ale nie rozumiem czego odejmujemy (x−y) , a nie np. dodajemy (x+y)

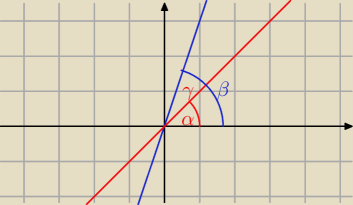
Janek191: γ = β − α

:l:

	√2		√2
Basiu ,ale chyba w tym przypadku jest x>y. Patrze na wykres tgx=		> −		= tgy
	2		2

Dziękuję wam już to zrozumiałem .

Basia: tu nie zajmujemy się kątami skierowanymi, tylko kątami wypukłymi z przedziału <0;180> tangens jest ujemny dla kątów rozwartych, a dodatni dla ostrych rozwarty > ostry

:l: