Oblicz kąt trójkąta matlamp: Dany jest trójkąt ABC. Wyznacz miarę kata ACB, jeżeli ortocentrum (tzn. punkt przecięcia wysokości)tego trójkąta należy do okręgu opisanego na trójkącie AOB, gdzie O jest środkiem okręgu opisanego natrójkącie ABC.

matlamp: prosze o pomoc!

Basia: wyszło mi, że γ=45 czy to poprawna odpowiedź?

Basia: oj chyba jednak nie; to zadanie dla Ety

Basia: policzyłam jeszcze raz; wyszło mi γ=60 cały kłopot w tym, że w ogóle nie wykorzystuję tej informacji o ortocentrum podejrzewam wobec tego, że gdzieś robię jakiś błąd

matlamp: Basia niestety właśnie nie mam dostępu do poprawnych odpowiedzi

Basia: znalazłam już błąd w swoich rachunkach; jeszcze pomyślę

matlamp: dzięki wielkie

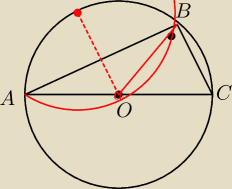
Basia: na pewno tak będzie gdy kąt ABC jest kątem prostym, bo wtedy ortocentrum tr. ABC to po prostu punkt B, który z pewnością należy do okręgu opisanego na tr.AOB co więcej wyszło mi, że tak musi być (spróbuję to narysować, ale nie wiem czy mi się uda) z tego jednak wynika, że nie da się ustalić miary kąta ACB takich trójkątów możesz przecież na średnicy AC oprzeć nieskończenie wiele i w każdym kąt ACB będzie miał inną miarę może chodziło jednak o kąt ABC ?

Basia: co do tego czy tak musi być mam jeszcze wątpliwości

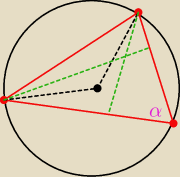
Adamm: skoro leżą na wspólnym okręgu, to kąt między wysokościami to 2α skąd z tego że w czworokącie kąty sumują się do 360^o, mamy α=60^o

Adamm: no chyba że jeden z kątów jest prostokątny, bo wtedy mamy nie 4 punkty na okręgu, ale 3 co opisała Basia

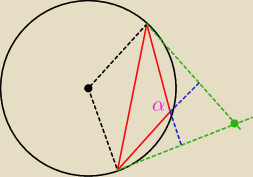
Adamm: tak samo dla rozwartych (bo rysunek nie rozpatrywał)

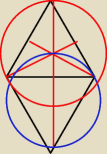
Basia: miara kąta ACB nie da się ustalić, to na pewno może być również trójkąt równoboczny

Basia: o nie widziałam wcześniej wpisów Adamma

Adamm: z tym rozwartokątnym, to wtedy przecież α nie jest rozwarty zrobiłem też rysunek, doszedłem do wniosku że dla rozwartokątnych taka sprawa zajść nie może

Adamm: (po objęciu jako α jednego kąta z podstawy)

Basia: z czego wynika, że kąt między wysokościami to 2α ? nie łapię tego

Basia: a dobrze już przecież widzę; wpisane oparte na tym samym łuku 180−γ=2y 3y=180 trapi mnie tylko dlaczego to nam pomija prostokątny

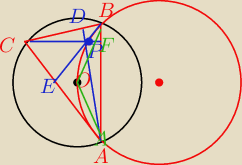
Basia: BPF=CPE = 90−γ₁ APF=CPD = 90−γ₂ APB = APF+BPF = 90−γ₁+90−γ₁ = 180−(γ₁+γ₂) = 180−γ AOB = 2γ AOB=APB 180−γ=2y 180=3γ y=60 to oczywiście obejmuje też trójkąt 30,60,90 ale warunki zadania spełnia każdy trójkąt, w którym β=90 i nie mogę dojść dlaczego to rozwiązanie jakoś tego nie sygnalizuje no bo jak się już wie to wiadomo, że trzeba rozważyć dwa przypadki 1. O∉AC 2. O∊AC ale dopóki się nie wie to co?

matlamp: Chodzi na pewno o kąt ACB, ciężkie zadanie

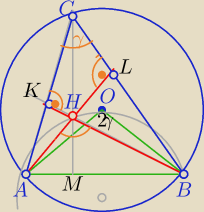
Mila: K,L,M − spodki wysokości ΔABC 1) ∡KHL=180^o−γ=∡AHB 2) ∡AOB=2γ jako kąt środkowy oparty na tym samym łuku co kąt wpisany ACB 3) ∡AHB=∡AOB jako kąty wpisane w okrąg ( opisany na AOB) oparte na tym samym łuku⇔ 180⁰−γ=2γ⇔3γ=180 γ=60^o =====