... Agata: Własności iloczynu skalarnego: Jeśli a jest wektorem niezerowym, a b jest wektorem dowolnym, to iloczyn skalarny tych wektorów jest równy iloczynowi modułu pierwszego wektora przez MIARĘ RZUTU DRUGIEGO WEKTORA NA OŚ PIERWSZEGO. Znalazłam takie twierdzenie w książce, patrząc na własności iloczynu skalarnego. Nie rozumiem tego twierdzenia − tego końca w szczególności. Umiałby ktoś je wytłumaczyć i zapisać je na wektorach? Z góry dziękuję bardzo.

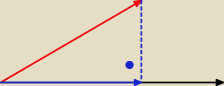
Adamm: iloczyn skalarny czarnego i czerwonego wektora to długość czerwonego razy długość niebieskiego

Adamm: poprawka iloczyn skalarny to długość niebieskiego razy czarnego

Adamm: o to w tym twierdzeniu chodzi

Agata: https://pl-static.z-dn.net/files/da2/d6cacb3a74ed4259ce22aa8ef05b58aa.jpg

Agata: 24.4 i 24.5 mogłby ktos mi tutaj to zapisac bardziej zrozumiale w sensie uwzglednic moduł l...l w zapisie − zapisac to na wektorach a i b (ze strzałka u gory), aby ten zapis był bardziej zrozumiały?

Adamm: a^→•b^→=|b^→|*|proj_a^→b^→| gdzie proj_a^→b^→ oznacza wektor będący rzutem prostopadłym a na b ("projekcją")