f kwadratowa Magda: mam wyznaczyc dziedzine rowniania i miejsca zerowe f(x)= x²−9/√x²−6x−7 wiec mianownik wiekszy lub rowny 0 poniewaz pod pierwiastkiem ale skoro to mianownik to nie moze sie rownac zero wiec zostaje wiekszy tylko czy i tak musze pisac najpierw z rowna sie i potem ze to jest dziedzina R\{cos} miejsca zerowe wyszly −1 i 7 wiec x ∊(−∞,−1) ∪ (7,∞) jest koncem zadania i i miejsca to wlasnie te −1 i 7

Basia:

	9
to jest f(x) = x2−
	√x2−6x−7

	x2−9
czy f(x) =		?
	√x2−6x−7

dziedzina jest dobrze; dalej nie

Maciess: Obstawiam że licznik to x²−9 Ułamek będzie 0 jeśli licznik będzie 0em x²−9=x²−3²

Basia: też tak obstawiam pierwsza wersja raczej dość trudna

Magda: wszystko w liczniku

Magda: czyli dobrze rozwiazalam?

Maciess: Obliczyłaś miejsca zerowe funkcji pod pierwiastkiem, która jest w mianowniku. Miejsce zerowe liczymy z licznika x²−9=0 x²−3²=0 (x−3)(x+3)−0 x=3 v x=−3 ...ale że pamiętam o dziedzinie to x=3 odpada. Miejsce zerowe to x = −3

Magda: jasne, czyli zerowe z licznika a dziedzina z mianownika jest w porzadku?

Magda: a jesli bylby sam pierwiastek, nie w ulamku i takie same polecenie to dziedzina z tego co pod pierwiastkiem ≥ 0 i tez to co pod nie rowna sie zero i wspolny przedzial?

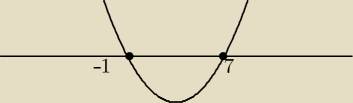
Maciess: "i tez to co pod nie rowna sie zero i wspolny przedzial?" nie rozumiem co tu masz na myśli, ale wszystko co wcześniej to prawda. Na tym konkretnym przykładzie to do dziedziny włączyłabyś jeszcze dwie liczby. −1 i 7 Pod pierwiastkiem może być tylko liczba dodatnia lub 0. Rozwiąze ten przykład dla jasności √x²−6x−7 Dziedzina x²−6x−7≥0 (x+1)(x−7)≥0 Patrze na rysunek i widze ze funkcja jest większa LUB równa 0 w przedziałach x∊(−∞;−1> U <7;+∞) Miejsca zerowe równiez widac na załączonym obrazku. Przepraszam za rysunek, ale nie umiem tu kreślic

Magda: rozumiem, o to mi chodziło