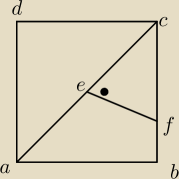
prostokąt proszę o wytłumacznie żw: Przekątne prostokąta ABCD mają długość 16 i przecinają się w punkcie E. Na boku BC obrano punkt F taki, że EF jest prostopadłe do AC i EF=6. Oblicz dł odc BF.

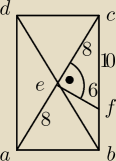Mateusz: z tw. pt |cf|=10 zauważamy, że trójkąty abc i fec są podobne (kkk) {|ac|}{

Mateusz: {ac}{cf}

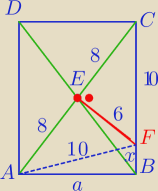Janek191: Mamy a² + ( 10 + x)² = 16² a² + x² = 10² ⇒ a² = 100 − x² −−−−−−−−−− 100 − x² + 100 + 20 x + x² = 256 20 x = 56 x = 2,8 ======

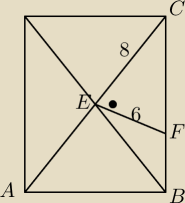Basia: tr.CBA ~ tr.CEF z Pitagorasa CF² = 100 CF=10

AC		BC
	=
CF		EC

16		BC
	=
10		8

BC = 8*1,6 = 12,8 BF = BC−CF = 12,8−10=2,8

Mateusz: ^ac_cf=^ab_ef ¹⁶₁₀=^ab₆ |ab|=9.6 z tw. pt w trójkącie abc oblicz |cb| a następnie |cb|−|cf|=|fb| odp to 2,8