trójkąt proszę o wytłumaczenie
holys: W trójkącie równoramiennym ABC dane są AB=8 AC=BC=10. Na boku BC obrano punkt D tak, że AD=AB.
Oblicz długość odcinka BD.
1 mar 22:40
Janek191:
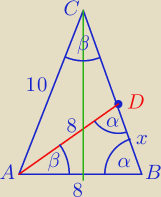
Δ ABD jest podobny do Δ ABC, więc
x = 6,4
======
1 mar 22:59
Basia:
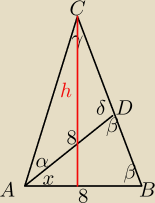
h
2+4
2=10
2
h
2 = 100−16 = 84
h =
√84 = 2
√21
| | h | | 2√21 | | √21 | |
sinβ= |
| = |
| = |
| |
| | BC | | 10 | | 5 | |
| | 2 | |
cosβ=√1−(21/25) = √4/25 = |
| |
| | 5 | |
BD
2 = 8
2+8
2 − 2*8*8*cos(x) =
64+64−128*cos(180−2β) =
128−128*(−cos(2β)) = 128+128*(cos
2β−sin
2β) =
| | 4 | | 21 | | 17 | | 17 | |
128+128*( |
| − |
| ) = 128−128* |
| = 128(1− |
| ) = |
| | 25 | | 25 | | 25 | | 25 | |
| | 8 | | 27*23 | | 210 | |
128* |
| = |
| = |
| |
| | 25 | | 25 | | 52 | |
wiem, że jakoś bez tw.cosinusów też się da to rozwiązać
1 mar 23:00
Eta:
No to
Janek Cię
Basiu ..........
1 mar 23:01
Basia: jak ja nie cierpię trójkątów podobnych
1 mar 23:02
Eta: 
1 mar 23:05