Przekątną prostopadłościanu
Wiktor: Przekątna prostopadłościanu o długości 12√3 tworzy z podstawą kąt o mierze 30 stopni.
Krawędzie podstawy są w stosunku 1:√2 .
Oblicz miary kątów, jakie tworzy przekątna prostopadłościanu z przekątnymi ścian bocznych
Proszę o wytłumaczenie, lub poradnik krok po kroku, żebym chociaż w jakiejś części mógł sam
zrobić.
1 mar 20:38
Basia:
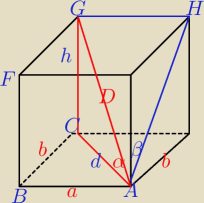
D=12
√3
α= 30
a
√2 = b
z tr.ABC
d
2 = a
2+b
2 = a
2+2a
2=3a
2
z tr.ACG
2h = D
h = 6
√3
d
2+h
2=D
2
3a
2+36*3 = 144*3
a
2+36 = 144
a
2 = 108
a
2 = 4*27 = 4*9*3
a = 2*3
√3 = 6
√3
b = 6
√3*
√2=6
√6
tr.GHA jest prostokatny
| | a | | 6√3 | | 1 | |
sinβ= |
| = |
| = |
| |
| | D | | 12√3 | | 2 | |
β=30
o
teraz dorysuj odc.AF
tr.AFG jest prostokatny
| | b | | 6√6 | | √2 | |
sinγ= |
| = |
| = |
| |
| | D | | 12√3 | | 2 | |
γ=45
o
posprawdzaj obliczenia
1 mar 20:52
xyz:
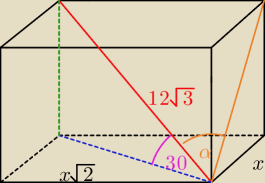
bez rysunku nic nie zrobisz.
1 mar 20:56