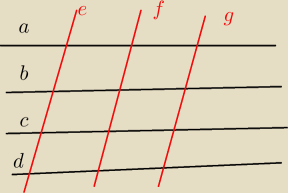
 Dane sa cztery proste rownolegle
Ile rownoleglobokow otrzymamy przecinajac te proste trzema prostymi rownoleglymi
Policzylem ze bedzie ich 18
Ale czy jest jakis sposob na policzenie ich gdyby tych prostych bylo duzo ?
Dane sa cztery proste rownolegle
Ile rownoleglobokow otrzymamy przecinajac te proste trzema prostymi rownoleglymi
Policzylem ze bedzie ich 18
Ale czy jest jakis sposob na policzenie ich gdyby tych prostych bylo duzo ?
|
| ||||||||||||||
* | =6*3=18 | ||||||||||||||
 Bo zeby byl rownoleglobok to musimy go utworzyc z dwoch poziomych i dwoch pionowych
Tylko oni chyba dali zeby bylo do policzenia bo to zadanie z 1 klasy serdniej .
Bo zeby byl rownoleglobok to musimy go utworzyc z dwoch poziomych i dwoch pionowych
Tylko oni chyba dali zeby bylo do policzenia bo to zadanie z 1 klasy serdniej .
| 4.3 | ||
− poziome dwie proste można wybrać na | = 6 sposobów, | |
| 2 |
| 3.2 | ||
− pionowe dwie proste można wybrać na | =3 sposoby, | |
| 2 |
