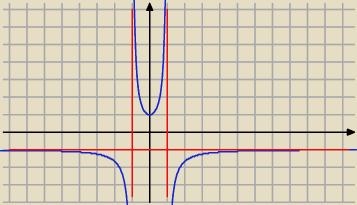
zadanka z analizy matematycznej Smoker: 1. Sformulowac twierdzenie Lagrange'a. 2. Korzystajac z definicji granicy udowodnic ze lim n/(n⁴+2)=0 n→∞ 3.Udowodnic, że równanie x³+x−3=0 ma dokladnie jedno rozwiązanie na przedziale (1,2) 4.Narysować wykres funkcji f(x)=(1+x²)/(1−x²) 5.Udowodnic rownosc arctgx+arctg (1−x)/1+x=π/4

PW: Nie wstawiaj tu takich "zadań": Sformułować twierdzenia Lagrange'a". Widzę, że chcesz mieć gotowca na kolokwium (egzamin?), bo wrzucasz takie urocze zestawy.

Blee: zadanie 4 mnie rozwaliło Coś takiego jest teraz na studiach ? Szczerze mówiąc −−− to poza tw. Lagrange'a (którego po prostu nie pamiętam ) reszta to jest spacerek ... góra 15 minut roboty

Basia: arctgx = y ⇔ tgy=x

	1−x		1−x
arctg		=z ⇔ tgz =
	1+x		1+x

stąd:

	1−tgy		tg(π/4)−tgy		π
tgz =		=		= tg(		−y)
	1+tgy		tg(π/4)+tgy		4

stąd:

	π
z =		−y
	4

	π
z+y =
	4

	π
y+z =
	4

	1−x		π
arctg(x)+arctg		=
	1+x		4

Basia: tw.Lagrange'a https://pl.wikipedia.org/wiki/Twierdzenie_Lagrange%E2%80%99a_(rachunek_r%C3%B3%C5%BCniczkowy)

Basia:

	n
|		−0|<ε ⇔
	n4+2

n
	<ε
n4+2

n		n		1
	<		=
n4+2		n4		n3

wystarczy więc aby

1		1		1
	<ε ⇔ 1<ε*n3 ⇔ n3>		⇔ n>
n3		ε		3√ε

czyli

	n		n
∀ε>0 ∃δ=1/3√ε ∀n>δ |		−0|<ε ⇒ limn→+∞		=0
	n4+2		n4+2

Basia: x³+x−3=0 f(1) = 1+1−3 = −1 f(2)= 8+2−1=5 na mocy własności Darboux ( https://pl.wikipedia.org/wiki/W%C5%82asno%C5%9B%C4%87_Darboux ) istnieje x₀∊(1,2) takie, że f(x₀)=0 czyli równanie x³+x−3=0 ma rozwiązanie w przedziale (1,2) jest to jedyne rozwiązanie ponieważ f'(x) = 3x²+1 >0 dla każdego x∊R czyli pochodna jest stale dodatnia ⇒ funkcja jest stale rosnąca czyli dla x<x₀ przyjmuje wartości <f(x₀)=0 a dla x>x₀ wartości >f(x₀)=0

Basia:

	1+x2
f(x) =
	1−x2

1−x²≠0 (1−x)(1+x)≠0 x≠−1 ∧ x≠1

	1   x2( +1)   x2
limx→±∞ f(x) = limx→±∞		=
	1   x2( −1)   x2

	1   +1 x2		0+1
limx→±∞		=		= −1
	1   −1 x2		0−1

funkcja ma asymptotę poziomą obustronną y= −1

	1+1
limx→−1−f(x) = [		] = −∞
	0−

	1+1
limx→−1+f(x) = [		] = +∞
	0+

	1+1
limx→1−f(x) = [		] = +∞
	0+

	1+1
limx→1+f(x) = [		] = −∞
	0−

mamy asymptoty pionowe x=−1 i x=1 nie ma asymptot ukośnych bo

	f(x)
limx→±∞		=0
	x

	2x(1−x2)−(−2x)(1+x2)		2x−2x3+2x+2x3
f'(x) =		=		=
	(1−x2)2		(1−x2)2

4x
(1−x2)2

	4
znak pochodnej jest taki jak znak funkcji y=x bo		jest stale dodatni
	(1−x2)2

x∊(−∞;−1)⇒ f'(x)<0 ⇒ f↘ x∊(−1;0) ⇒ f'(x)<0 ⇒ f↘ x∊(0;1) ⇒ f'(x)>0 ⇒ f↗ x∊(1;+∞) ⇒ f'(x)>0 ⇒ f↗ czyli dla x=0 mamy minimum lokalne = f(0)=−1 tabelka i wykres