K Kasia: Wyznacz kat rozwarcia stozka ktorego tworzaca ma dlugosc 10cm, a pole podstawy jest rowne (50+25√2)pi cm²

Kasia: 🙄

Dero2005: Oblicz średnicę podstawy, zastosuj wzór cosinusów

Kasia: Zrobilam tam i wyszlo mi ze cos rowna sie 4−√2 przez 4

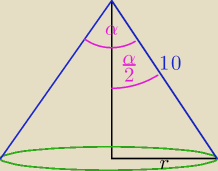
xyz: α − kat rozwarcia stozka Pp = πr² = (50+25√2)π cm² zatem r² = 50+25√2 = 25(2+√2) r = √25(2+√2) = 5 √2+√2, bo r > 0 teraz albo z twierdzenia cosinusow (wg mnie latwiej) albo z sinusa kata, tylko wtedy bierzemy polowke tego kata to ktora metoda? Mialas tw. cos. ?

Kasia: Ja zrobilam z twierdzenia i napisalam wyzej wynik jaki mi wyszedl i nie wiem za bardzo co dalrj

xyz: tw. cos. (2r)² = 10² + 10² − 2*10*10*cosα 4r² = 100 + 100 − 200cosα 4*(50+25√2) = 200 − 200cosα 200cosα = 200 − 4*(5+25√2)

	200 − 4*(5+25√2)		200−20−100√2		9		√2
cos α =		=		=		−
	200		200		10		2

Dero2005: P = (50+25√2)π = πr² r² = 25(2+√2) l = 10 (2r)² = 2l² − 2l²cosα

	√2
cosα = −
	2

α = 135^o