Pole koła 1234: Dany jest prostokąt o bokach 20 i 20√2. Wyznacz pole zacieniowanego obszaru. Obrazek w linku: https://imgur.com/a/aLA47

1234: czy ktoś może naprowadzić?

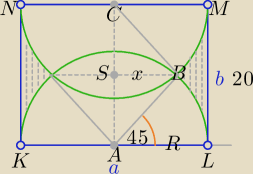
Mila: a=20√2 b=20 R=10√2 R²=|AS|²+y²⇔(10√2)²=10²+x² x=10⇔∡SAB=45^o P_ALMC=10√2*20=200√2

	1
PABC=		*20*10=100
	2

	45		1
Pwyc.LAB=		π*R2=		*200*π=25π
	360		8

P_z=2*P_LBM=2*[200√2−(100+2*25π)]=2*(200√2−100−50π)= =20*(20√2−10−5π)≈51.6 Posprawdzaj rachunki.

Mila: Może Eta policzy jeszcze inaczej

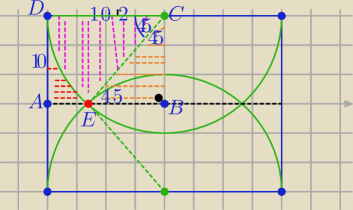Eta: P(AED)= P(ABCD)− P(EBC) − P(wycinkaDCE) P(ABCD)= 10*10√2= 100√2 ΔEBC jest równoramienny i prostokątny ( bo |EC|=10√2 i |CB|=AD|=10 to |EB|=10 kąt DCE =45^o zatem P(ΔEBC)=0,5*10*10=50

	1		1
P(wycinkaDCE)=		πr2 =		*(10√2)2π= 25π
	8		8

Pole wszystkich części zakreskowanych ( na Twoim rys): to 4*P = 4* (100√2−50−25π) = 100(4√2−2−π) ============

Eta: No i zgadza się u Mili wyłączyć jeszcze 5 przed nawias P=100(4√2−2−π)