kwadraty liczb marek: Sprawdz czy liczby 3x+1, 4x+1, 6x+1 mogą być kwadratami liczb dla x>0

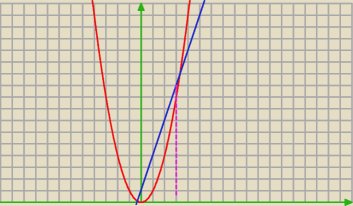
PW: Powiem więcej, istnieje taka x>0, że 3x+1=x². "Więcej", bo po prawej stronie wcale nie musi być x^, mógł być kwadrat dowolnej liczby.

Adamm: czy x jest naturalne? inaczej to raczej bez sensu

PW: Doszukujesz się bezsensu poza treścią zadania. Jeżeli marek zgubił słowo "naturalnych", to niech teraz posypie głowę popiołem.

marek: tak było kwadratami liczb naturalnych sorry

PW: k²=3x+1, k∊N i x∊N. k²−1=3x (k−1)(k+1)=3x. Prawa strona jest podzielna przez 3, zatem musi być podzielna też lewa strona, a więc jedna z liczb k−1,k+1. Jeżeli k−1=3p, p∊N, to k+1=3p+2 i mamy (1) 3p(3p+2)=3x. Jeżeli k+1=3r, to k−1=3r−2 i równość ma postać (2) 3r(3r−2)=3x, Sprawdzenie − dla (1) jest 3x+1=3p(3p+2)+1=9p²+6p+1=(3p+1)²=k², − dla (2) jest 3x+1=3r(3r−2)+1=9r²−6r+1=(3r−1)²=k². W obydwu wypadkach liczba 3x+1 jest kwadratem liczby naturalnej. Odpowiedź: Jeżeli wziąć x=p(3p+2) lub x=r(3r−2) dla naturalnych p lub r, to liczba 3x+1 jest kwadratem liczby naturalnej.

Basia: Sensu w tym zadaniu nie widzę. Jeżeli x może być dowolną liczbą rzeczywistą dodatnią, jest oczywiste, że 3x+1 (i pozostałe również) może sobie być kwadratem każdej liczby naturalnej n≥2 3x+1=n² 3x= n²−1

	n2−1
x =
	3

i nawet nie trzeba, żeby n²−1 było podzielne przez 3 przykład: n=3

	9−1		8
x =		=
	3		3

3x+1 = 8+1=9=3²