kąty trójkąta Marcin: W trójkącie równoramiennym ABC ,|AC\=|BC|na podstawie obrano punkt D tak,że |AD|=2|DB| Wiedząc,że kąt ACD jest kątem prostym wyznacz miary kątów trójkąta ABC

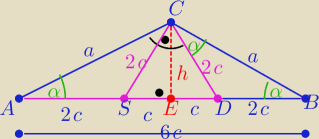
Eta: 1/ jak zwykle rysunek zgodny z treścią zadania 2/................ komentarze zostawiam już Tobie Marcinie ................... 3α+90^o=180^o ⇒ α=30^o Kąty trójkąta ABC mają miary .................. i to tyle

Krzysiek60: A jakie tutaj komentarze potrzebne ?

Krzysiek60: Podbijam

iteRacj@: |AC|=|BC| → kąty przy podstawie ΔABC są równe |<CAB|=|<CBA|=α z ΔACD |<CDA|=90⁻α ΔACD∼ΔCDE∼ΔBCE (kkk)

	c		h
stąd		=		=tg α
	h		c+2c

h=√3*c z tw. PItagorasa w ΔCDE → |CD|=2c więc ΔCDB równoramienny i |<DCB|=|<DBC|=α czyli w ΔABC 3α+90^o=180^o

Krzysiek60: Dobrze iteRacj@

Eta: Hej bez żadnych podobieństw ( choć można , jak ktoś "lubi" Można też dodać taki komentarz: 1/ trójkąt ACD prostokątny na nim można opisać okrąg o promieniu 2c to |SC|=R=2c 2/ to trójkąt SCD jest równoboczny o boku "2c" zatem |<SCD|=60^o ⇒ |<ACS|=|<CAS|= |<DCB|=|<DBC|=90^o−60^o= 30^o to w trójkącie ABC kąty mają miary, 30^o,30^o, 120^o Pozdrawiam Krzyśka i Rację iterrr

iteRacj@: @Eta pisałam to tak jak maturę z polskiego jak nie zgadnę, co autor miał na myśli, to mnie obleją i nie wstrzeliłam się w klucz

Eta:

Krzysiek60: Dziekuje Eta Pozdrawiam