Twierdzenie cosinusow
Krzysiek60:
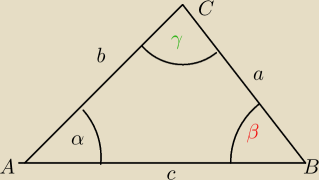
Twierdzenie cosinusow mowi ze
a
2= b
2+c
2−2bc* cosα
W tablicach mam dalej ze
| | 1 | |
Moglbym to z rozumiez ze b2+c2= (b+c)2−2bc −2bc= −4bc ale skad cos2 |
| α? |
| | 2 | |
28 lut 17:45
Blee:
cosα = 2cos2(α/2) − 1
więc:
2bc*cosα = 4*bc*cos2(α/2) − 2bc
28 lut 17:49
jc: cos α = 1 − 2sin2α/2 = 2cos2α/2 − 1
28 lut 17:50
Krzysiek60: czesc
no dobrze a ten drugi ?
28 lut 17:56
Blee:
analogicznie tylko masz
cosα = 1 − 2sin2(α/2)
2bc*cosα = 2bc − 4bc*sin2(α/2)
28 lut 18:00
Krzysiek60: To ja chyba zapomnialem
Ale wrocmy jescze do tego rysunku i do tablic ktore mam
Wzor a= b*cosγ+c*cosβ
Skad to ?
28 lut 18:00
Adamm:
wysokość prowadzimy z kąta α, i ona dzieli a na dwie części
a=a
1+a
2
skąd wzór
28 lut 18:03
Adamm:
no chyba że wysokość nie leży na boku a
to wtedy trzeba trochę inaczej
28 lut 18:05
Krzysiek60: czyli ?
28 lut 18:06
Adamm:
b2=a2−2cosβ*a*c+c2
c2=a2−2cosγ*a*b+b2
dodajemy, dzielimy przez 2a
mamy nasz wzór (po uporządkowaniu)
tak też można
28 lut 18:08
Krzysiek60: Czesc
jc
Znalazlem te wzory
28 lut 18:10
Krzysiek60: Dziekuje
Adamm
28 lut 18:11