równanie trygonometryczne DonLotario: Siemka, nauczycielka pokazała nam jak rozwiązać równanie trygonometryczne z cosinusem, w przypadku gdy te funkcje przyrównamy do liczby ujemnej: np. cosα=−^√3₂ 1)korzystamy z wzoru redukcyjnego cos(π−α)=−cosα 2)π−α=^π₆ +2kπ lub π−α=(−^π₆)+2kπ czyli α=^5π₆+2kπ lub α=^7π₆+2kπ Problem w tym ze mi sie to rachunkowo nie zgadza, czy to jest w ogole poprawna metoda? czy ja sie myle i cos zle licze?

Krzysiek60: A po co tutaj wzor redukcyjny ? To jest rownanie elelemtrarne cosx=K rozwiazanie tego rownania to x= α+2kπ lub x= −α+2kπ

Mila: Ja rozwiązuję tak:

	√3
cosα=−
	2

	π		π
α=		+π+2kπ lub α=−		+π+2kπ
	6		6

	7π		5π
α=		+2kπ lub α=		+2kπ
	6		6

DonLotario: a jak mamy „π−α=π6 +2kπ lub π−α=(−π6)+2kπ” to nie wyjdzie dobry wynik? xzyli ta cala metoda jest zla? Przepisywalem to z kserowki wiec nie popelnilem bledu przy przepisywaniu../

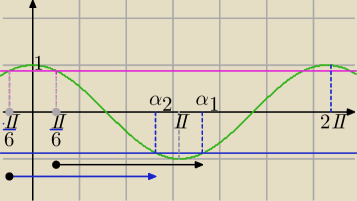
Mila: Przecież masz taki sam wynik. Ja korzystam z rozwiązania równania :

	√3
cosx=		i dodaję π
	2

DonLotario: chodzilo mi o to ze jak wyliczysz z tego α(z równosci ktora napisalem na samym poczatku) to mamy α=^7π₆−2kπ lub α=^7π₆−2kπ co jest niezgodne i w dodatku gmatwa mi wszystko

Krzysiek60: https://matematykaszkolna.pl/strona/4864.html

Mila: Cosinus jest funkcją parzystą, zatem cos(π−x)=cos(x−π)=−cosx Skorzystaj z tego, będziesz miał:

	π		π
α−π=		+2kπ lub α−π=(−		)+2kπ
	6		6

	7π		5π
α=		+2kπ lub α=		+2kπ
	6		6

I to jest sposób, który podałam.

DonLotario: O dzieki, o to mi sie od poczatku rozchodzilo

Mila: