proszę o rozwiązanie
Anna: | | sinx − I cosx I | |
narysuj wykres funkcji f(x) = |
| |
| | cosx | |
zrobiłam dziedzinę
| | π | |
cosx ≠ 0 czyli x ≠ |
| + 2kπ |
| | 2 | |
| | sinx | | IcosxI | |
f(x) = |
| − |
| |
| | cosx | | cosx | |
28 lut 10:13
Jerzy:
1) Popraw dziedzinę
2) Dla cosx > 0 masz: f(x) = tgx − 1
Dla cosx < 0 masz: f(x) = tgx + 1
28 lut 10:23
Anna: czy chodzi o dopisanie dla k ∊ C
28 lut 10:33
Anna: przepraszam że nie napisałam pełny tekst zadania
| | sinx − IcosxI | | π | | π | |
Narysuj wykres funkcji f(x) = |
| dla x ∊ (0 ; |
| )∪ ( |
| ;π) |
| | cos | | 2 | | 2 | |
Odczytaj z wykresu rozwiązania nierówności f(x) ≥ 0
28 lut 10:48
aniabb:
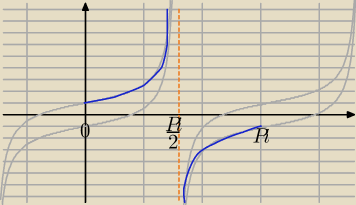
to niebieskie
28 lut 11:26
Anna: punkt przecięcia z osią OY to1 i −1
28 lut 11:42
aniabb: 1 te szare to pomocnicze ... pisałam że TYLKO NIEBIESKIE
28 lut 11:46
Anna: dziękuję
28 lut 22:13