bryły, kula wpisana w bryłę sage: Jaki jest stosunek objętości kuli do objętości graniastosłupa prawidłowego czworokątnego opisanego na tej kuli, jeśli przekrój ostrosłupa zawierający dwie jego boczne krawędzie jest trójkątem prostokątnym?

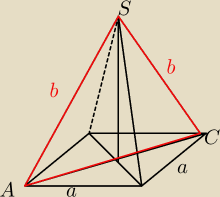
Basia: d − przekątna podstawy d²=a²+a²=2a² d = a√2 b²+b²=2a² 2b²=2a² b=a H²+(d/2)² = b²

	2a2
H2+		= a2
	4

	a2		a2
H2 = a2−		=
	2		2

	a
H =
	√2

	1		1		a		a3
Vo =		a2*H =		*a2*		=
	3		3		√2		3√2

środek kuli jest też środkiem okręgu wpisanego w tr. ASC a ponieważ jest to trójkąt prostokątny

	b+b−d		a+a−a√2		2a−a√2		a(2−√2)
r=		=		=		=
	2		2		2		2

	4		a3(2−√2)3		a3(2−√2)3π
Vk =		*π*		=
	3		8		3*2

Vo		a3		3*2		2
	=		*		=		=
Vk		3√2		a3(2−√2)3		√2(2−√2)3

2		2		1
	=		=
√2*[√2(√2−1)]3		4(√2−1)3		2(√2−1)3

sprawdzaj obliczenia, bo moglam się pomylić

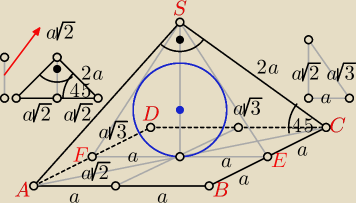
Bogdan: Środek kuli wpisanej w ostrosłup prawidłowy czworokątny jest środkiem okręgu wpisanego w trójkąt FES o bokach długości: 2a, a√3, a√3.

Jerzy: Basiu .... "środek kuli jest też środkiem okręgu wpisanego w tr. ASC" ... to nieprawda.

Basia: Nieprawda, za późno już było, to miał być tak jak narysował Bogdan tr.ESF

Mila: Treść − najpierw graniastosłup, potem ostrosłup i brak zainteresowania