Dany jest ostrosłup ABCD takim że |AB|=|CD|=2a
siemanko: Dany jest ostrosłup ABCD taki że |AB|=|CD|=2a i |BC|=|BD|=|AC|=|AD| oraz |ACB|=2α. Uzasadnij,
że objętość V=
2a3√cos2α3sinα
Bardzo proszę o pomoc

Mila:
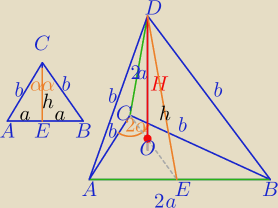
1) W ostrosłupie trójkątnym dwie krawędzie skośne maja długość 2a.
2) ściany są przystającymi Δ równoramiennymi.
Długość: h =a*ctgα
| | 1 | |
PΔABC= |
| *2a*a*ctgα=a2*ctgα |
| | 2 | |
4)
|DO|=H, |DE|=h=a *ctgα
W DOC: (2a)
2=|OC|
2+H
2⇔4a
2=x
2+H
2
W ΔDOE: h
2=(h−OC)
2+H
2⇔
|OC|=x⇔h
2=h
2−2hx+x
2+H
2⇔
H
2+x
2=2hx i
H
2+x
2=4a
2⇔2hx=4a
2
hx=2a
2⇔
H
2=4a
2−x
2
| | 1 | |
H2=4a2*(1− |
| )=4a2*(1−tg2α) |
| | ctg2α | |
| | sin2α | | cos2α−sin2α | |
H2=4a2*(1− |
| )=4a2* |
| |
| | cos2α | | cos2α | |
5)
| | 1 | | 2a | |
V= |
| *a2*ctgα* |
| *√cos2α⇔ |
| | 3 | | cosα | |
==================

