 Można tak ( bez tw. cosinusów)
Mamy wykazać ,że
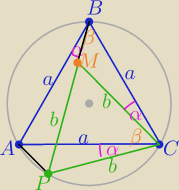
|PB|=|PA|+|PC|
Na odcinku BP wybieramy punkt M tak,że ΔCPM jest równoboczny o boku "b"
to α+β= 60o ⇒ |<BCM|=60o−β= α
Kąty ABP i ACP mają równe miary α bo są wpisane oparte na tym samym łuku AP
zatem trójkąty ACP i BMC są przystające z cechy (kbk)
czyli |AP|=|BM|
i mamy tezę:
|PB|=|BM|+|MP|= |PA|+b
|PB| = |PA|+|PC|
c.n.w
Można tak ( bez tw. cosinusów)
Mamy wykazać ,że
|PB|=|PA|+|PC|
Na odcinku BP wybieramy punkt M tak,że ΔCPM jest równoboczny o boku "b"
to α+β= 60o ⇒ |<BCM|=60o−β= α
Kąty ABP i ACP mają równe miary α bo są wpisane oparte na tym samym łuku AP
zatem trójkąty ACP i BMC są przystające z cechy (kbk)
czyli |AP|=|BM|
i mamy tezę:
|PB|=|BM|+|MP|= |PA|+b
|PB| = |PA|+|PC|
c.n.w