Kat dwuścienny pomocy
Wojtek: Pomocy! Cała klasa nie potrafi tego rozwiązać. Zadanie 14/121 Zbiór zadań Nowa Era 3:
Wyznacz sinus kąta nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do
płaszczyzny podstawy, jeżeli kąt dwuścienny między sąsiednimi ścianami bocznymi ma miarę 2α
Odpowiedź: √2 cosα
27 lut 08:53
Bogdan:
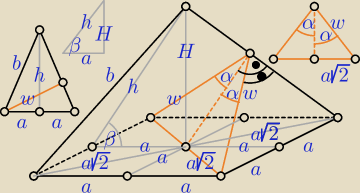
| a√2 | | a√2 | | 2a2 | |
| = sinα ⇒ w = |
| ⇒ w2 = |
| i a2 = h2 − H2 |
| w | | sinα | | sin2α | |
b
2 = H
2 + 2a
2 = H
2 + 2h
2 − 2H
2 = 2h
2 − H
2
| | 1 | | 1 | |
Pole ściany bocznej |
| bw = ah ⇒ |
| b2w2 = a2h2 |
| | 2 | | 4 | |
| 1 | | 2a2 | |
| (2h2 − H2)* |
| = a2h2 /:a2 |
| 4 | | sin2α | |
| 2h2 − H2 | |
| = h2 ⇒ 2h2 − H2 = 2h2sin2α ⇒ 2h2(1 − sin2α) = H2 /:h2 |
| 2sin2α | |
| H2 | |
| = 2cos2α ⇒ sin2β = 2cos2α |
| h2 | |
27 lut 12:52
Wojtek: Dziękuję za pomoc
28 lut 08:19
Eta:
Długo dziękował.... ale podziękował
28 lut 22:20
Eta:
Ode mnie ...........
dla
Bogdana
28 lut 22:23