Wyznacz zbiór wartości funkcji f załamka: Wyznacz zbiór wartości funkcji f:

	1
f(x)=
	cosx

xe<^3pi₄,^4pi₃> Rozwiązane jest tak:

	4pi
Największą wartość jaką cosx przyjmuje w danym przedziale, to przy		jest −12, a
	3

najmniejszą wartość przyjmuje −1 dla pi, stąd wychodzi mi ZWe<−2;−1>, oczywiście po podstawieniu tych wartości do f(x) W odpowiedziach jest ZWe<−2;^2√3₃> Gdzie mam błąd?

kas:

	4pi		√3
cos		= −
	3		2

zobacz wzory redukcyjne

załamka: cos240=cos(pi+60)=−cos60=−¹₂ Chyba nie tu jest błąd, coś jest "nie tak" z tą jedynką...

Basia: nie masz błędu, o ile dobrze przepisałaś treść zadania

załamka: Jest to zdanie 2.59 z 3 części Pazdro Nie ma błędu w treści, czy w takim razie odpowiedzi są błędne?

Basia: na to wygląda zdarzają się błędy w druku

PW:

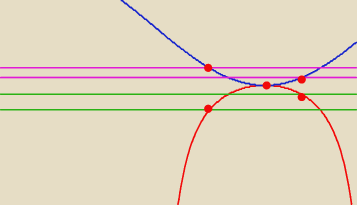
	3π		4π		3π
Na przedziale <		,		są trzy szczególne punkty: lewy kraniec		, prawy
	4		3		4

	4π
kraniec		oraz punkt, w którym funkcja cos osiąga minimum, czyli π.
	3

	3π		π		π		√2
cos		=cos(π−		)=−cos		=−
	4		4		4		2

	4π		π		π		√3
cos		=cos(π+		)=−cos		=−
	3		3		3		2

cosπ=−1. Spełnione są nierówności:

	√3		√2
−1<−		<−
	2		2

a dla odwrotności

	2		2
−1>−		>−
	√3		√2

	2√3
−1>−		>−√2
	3

	1
Maksimum funkcji		jest −1, a minimum −√2.
	cosx

	2√3
Liczba −		jest wartością w prawym krańcu przedziału, ale nie jest maksimum.
	3

Eta: Mała uwaga cos(4π/3)= −cos(π/3)= −1/2

PW: A ja głupi spojrzałem na 21:23 i uwierzyłem ! Coraz gorzej z koncentracją.

załamka: Dziękuję wszystkim za pomoc